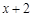题目内容
由表格中的数据可以判定方程ex-x-2=0的一个零点所在的区间(k,k+1)(k∈N),则k的值为( )| x | -1 | 1 | 2 | 3 | |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
A.0
B.1
C.2
D.3
【答案】分析:设f(x)=ex-x-2.根据表格中的数据,可以判定函数f(x)=ex-x-2中,自变量x分别取-1,0,1,2,3时,函数的值,然后根据零点存在定理,我们易分析出函数零点所在的区间,进而求出k的值.
解答:解:设f(x)=ex-x-2.根据表格中的数据,
我们可以判断f(-1)<0;f(0)<0;f(1)<0;f(2)>0;f(3)>0;
根据零点存在定理得
在区间(1,2)上函数存在一个零点
此时k的值为1
故选B.
点评:本题考查的知识点是函数的零点,其中根据表格中数据判断自变量x分别取-1,0,1,2,3时函数的值的符号,是解答本题的关键.
解答:解:设f(x)=ex-x-2.根据表格中的数据,
我们可以判断f(-1)<0;f(0)<0;f(1)<0;f(2)>0;f(3)>0;
根据零点存在定理得
在区间(1,2)上函数存在一个零点
此时k的值为1
故选B.
点评:本题考查的知识点是函数的零点,其中根据表格中数据判断自变量x分别取-1,0,1,2,3时函数的值的符号,是解答本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 的一个零点所在的区间是
的一个零点所在的区间是 ,则
,则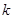 的值为
的值为