题目内容
已知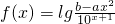 ,函数y=f(x)与函数y=g(x)满足如下对应关系:当点(x,y)在y=f(x)的图象上时,点
,函数y=f(x)与函数y=g(x)满足如下对应关系:当点(x,y)在y=f(x)的图象上时,点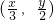 在y=g(x)的图象上,且f(0)=0,g(-1)=1.
在y=g(x)的图象上,且f(0)=0,g(-1)=1.
(1)求函数y=g(x)的解析式;
(2)指出函数y=g(x)的单调递增区间,并用单调性定义证明之.
解:(1)由题意可得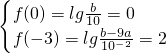 ,解得
,解得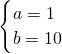 ,
,
故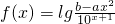 =
=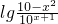 ,x∈(
,x∈( ,
, )
)
故必有2y=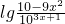 ,即y=
,即y=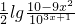 ,
,
故函数y=g(x)的解析式为:g(x)=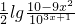 ;
;
(2)由(1)可知,函数y=g(x)的单调递增区间为( ,0),
,0),
任取x1,x2∈( ,0),且x1<x2,
,0),且x1<x2,
由复合函数的单调性可知,只需证明函数m(x)=10-9x2在区间( ,0)上单调递增,
,0)上单调递增,
则有m(x1)-m(x2)=(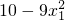 )-(
)-(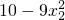 )
)
=9(x2+x1)(x2-x1),
∵x1,x2∈( ,0),且x1<x2,
,0),且x1<x2,
∴x2+x1<0,x2-x1>0,∴9(x2+x1)(x2-x1)<0,
故m(x1)<m(x2),
故函数y=g(x)的单调递增区间为( ,0),
,0),
分析:(1)由题意可得关于ab的方程组,解之可得函数f(x)的解析式,进而可得g(x)的解析式;
(2)可知函数的单调递增区间为( ,0),由复合函数的单调性,只需证明函数m(x)=10-9x2在区间(
,0),由复合函数的单调性,只需证明函数m(x)=10-9x2在区间( ,0)上单调递增即可,由单调性的定义可证.
,0)上单调递增即可,由单调性的定义可证.
点评:本题考查函数解析式的求解,涉及函数单调性的判断与证明,属基础题.
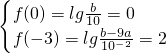 ,解得
,解得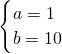 ,
,故
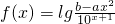 =
=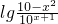 ,x∈(
,x∈( ,
, )
)故必有2y=
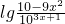 ,即y=
,即y=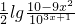 ,
,故函数y=g(x)的解析式为:g(x)=
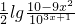 ;
;(2)由(1)可知,函数y=g(x)的单调递增区间为(
 ,0),
,0),任取x1,x2∈(
 ,0),且x1<x2,
,0),且x1<x2,由复合函数的单调性可知,只需证明函数m(x)=10-9x2在区间(
 ,0)上单调递增,
,0)上单调递增,则有m(x1)-m(x2)=(
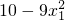 )-(
)-(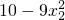 )
)=9(x2+x1)(x2-x1),
∵x1,x2∈(
 ,0),且x1<x2,
,0),且x1<x2,∴x2+x1<0,x2-x1>0,∴9(x2+x1)(x2-x1)<0,
故m(x1)<m(x2),
故函数y=g(x)的单调递增区间为(
 ,0),
,0),分析:(1)由题意可得关于ab的方程组,解之可得函数f(x)的解析式,进而可得g(x)的解析式;
(2)可知函数的单调递增区间为(
 ,0),由复合函数的单调性,只需证明函数m(x)=10-9x2在区间(
,0),由复合函数的单调性,只需证明函数m(x)=10-9x2在区间( ,0)上单调递增即可,由单调性的定义可证.
,0)上单调递增即可,由单调性的定义可证.点评:本题考查函数解析式的求解,涉及函数单调性的判断与证明,属基础题.

练习册系列答案
相关题目