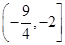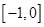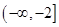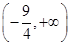题目内容
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为 ( )
A.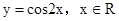 | B.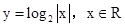 且x≠0 且x≠0 |
C.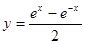 , x , x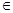 R R | D.y=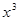 +1, x +1, x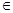 R R |
B
解析试题分析:判断函数的奇偶性,首先应看定义域是否关于原点对称,偶函数满足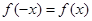 .本题选项中,是偶函数的有
.本题选项中,是偶函数的有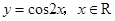 ,
, 且
且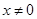 ,但只有
,但只有 且
且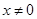 在区间(1,2)内是增函数,故选B.
在区间(1,2)内是增函数,故选B.
考点:函数的奇偶性、单调性

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知定义域为R的函数f(x)在区间(8,+∞)上为减函数,且函数y=f(x+8)为偶函数,则
| A.f(6)>f(7) | B.f(6)>f(9) |
| C.f(7)>f(9) | D.f(7)>f(10) |
设f(x)= 则下列结论正确的是( )
则下列结论正确的是( )
A. | B. | C. | D. |
定义在 上的函数
上的函数 满足
满足 (
( ),
), ,则
,则 等于( )
等于( )
| A.2 | B.3 | C.6 | D.9 |
函数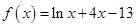 的零点一定位于区间( )
的零点一定位于区间( )
| A.(1, 2) | B.(2, 3) | C.(3, 4) | D.(4, 5) |
下列函数,在其定义域中,既是奇函数又是减函数的是
A. | B. | C. | D. |
设 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在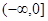 上是增函数,设
上是增函数,设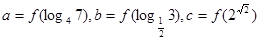 ,则
,则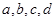 的大小关系是( )
的大小关系是( )
A.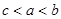 | B.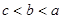 | C.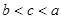 | D.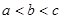 |
若关于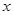 的方程
的方程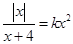 有四个不同的实数解,则
有四个不同的实数解,则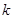 的取值范围为 ( )
的取值范围为 ( )
A.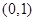 | B.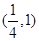 | C. | D.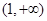 |
 与
与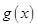 是定义在同一区间
是定义在同一区间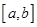 上的两个函数,若函数
上的两个函数,若函数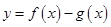 在
在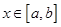 上有两个不同的零点,则称
上有两个不同的零点,则称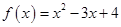 与
与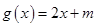 在
在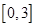 上是“关联函数”,则
上是“关联函数”,则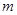 的取值范围为 ( )
的取值范围为 ( )