题目内容
在自然数集N中,被3除所得余数为r的自然数组成一个“堆”,记为[r],即[r]={3k+r|k∈N},其中r=0,1,2,给出如下四个结论:
①2011∈[1];②若a∈[1],b∈[2]则a+b∈[0];③N=[0]∪[1]∪[2];④若a,b属于同一“堆”,则a-b不属于这一“堆”.
其中正确结论的个数( )
①2011∈[1];②若a∈[1],b∈[2]则a+b∈[0];③N=[0]∪[1]∪[2];④若a,b属于同一“堆”,则a-b不属于这一“堆”.
其中正确结论的个数( )
分析:根据题中“堆”的理解,在整数集Z中,被3除所得余数为r的所有整数组成一个“堆”,对于各个结论进行分析:①∵2011÷3=670…1;②a∈[1],b∈[2]则=3k+1,b=3m+2,a+b=3(k+m)+3=3(k+m+1),即a+b∈[0],故②正确;③整数集中的数被3除的数可以且只可以分成三类,故Z=[0]∪[1]∪[2];④从正反两个方面考虑即可.
解答:解:①∵2011÷3=670…1,∴2011∈[1],故①正确;
②a∈[1],b∈[2]则a=3k+1,b=3m+2,a+b=3(k+m)+3=3(k+m+1),即a+b∈[0],故②正确;
③∵整数集中的数被3除的数可以且只可以分成三类,故Z=[0]∪[1]∪[2],故③正确;
④∵整数a,b属于同一“堆”,∴整数a,b被3除的余数相同,从而a-b被3除的余数为0,
当a,b都属于[0]时,则有a-b∈[0],故④错误.
∴正确结论的个数是3.
故选C.
②a∈[1],b∈[2]则a=3k+1,b=3m+2,a+b=3(k+m)+3=3(k+m+1),即a+b∈[0],故②正确;
③∵整数集中的数被3除的数可以且只可以分成三类,故Z=[0]∪[1]∪[2],故③正确;
④∵整数a,b属于同一“堆”,∴整数a,b被3除的余数相同,从而a-b被3除的余数为0,
当a,b都属于[0]时,则有a-b∈[0],故④错误.
∴正确结论的个数是3.
故选C.
点评:本题主要考查了选修3同余的性质,具有一定的创新,关键是对题中“堆”的理解解,属于创新题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
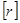 ,即
,即 ,其中
,其中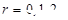 ,给出如下四个结论:
,给出如下四个结论: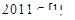 ②若
②若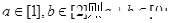 ;③
;③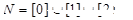
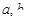 属于同一“堆”,则
属于同一“堆”,则 不属于这一“堆”其中正确结论的个数 ( )
不属于这一“堆”其中正确结论的个数 ( ) 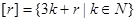 ,其中
,其中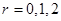 ,给出如下四个结论:
,给出如下四个结论: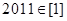 ②若
②若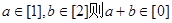 ;③
;③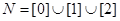 ④若
④若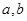 属于同一“堆”,则
属于同一“堆”,则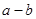 不属于这一“堆”其中正确结论的个数 (
)
不属于这一“堆”其中正确结论的个数 (
)