题目内容
方程x2+ax+2=0至少有一个实数根小于-1,则实数a的取值范围为 .
{a|2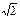 ≤a<+∞,且a≠3}
≤a<+∞,且a≠3}
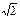 ≤a<+∞,且a≠3}
≤a<+∞,且a≠3}设f(x)=x2+ax+2,其图象是过定点(0,2),开口向上的抛物线.
(1)当原方程只有一 实根小于-1时,必须满足f(-1)=(-1)2+(-1)a+3<0.∴a>3.
实根小于-1时,必须满足f(-1)=(-1)2+(-1)a+3<0.∴a>3.
(2)当原方程的两个实根都小于-1时,必须满足 解得2
解得2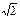 ≤a<3.
≤a<3.
(1)当原方程只有一
 实根小于-1时,必须满足f(-1)=(-1)2+(-1)a+3<0.∴a>3.
实根小于-1时,必须满足f(-1)=(-1)2+(-1)a+3<0.∴a>3.(2)当原方程的两个实根都小于-1时,必须满足
 解得2
解得2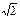 ≤a<3.
≤a<3.
练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
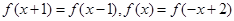 ,方程
,方程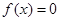 在
在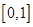 内有且只有一个根
内有且只有一个根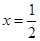 ,则
,则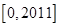 内根的个数为
内根的个数为 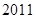
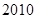
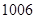
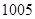
 是定义在区间
是定义在区间 上的函数,且
上的函数,且 ,则方程
,则方程 在区间
在区间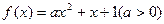 的两个不同的零点为
的两个不同的零点为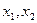
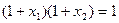 ;
; 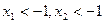 ;
;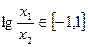 ,试求
,试求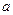 的取值范围.
的取值范围.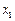 是方程
是方程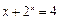 的根,
的根,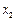 是方程
是方程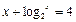 的根,则
的根,则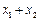 的值是_______.
的值是_______.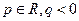 ,当函数
,当函数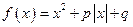 的零点多于1个时,
的零点多于1个时,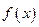 在以其最小零点与最大零点为端点的闭区间上的最大值为_____________.
在以其最小零点与最大零点为端点的闭区间上的最大值为_____________. 有一个零点是2,则二次函数
有一个零点是2,则二次函数 的零点是 。
的零点是 。