题目内容

平面直角坐标系xOy中，已知向量
AB
=(6，1)，
BC
=(x，y)，
CD
=(-2，-3)，且
AD
∥
BC
．
（1）求x与y之间的关系式；
（2）若
AC
⊥
BD
，求四边形ABCD的面积．
分析：（1）由
AD
∥
BC
，结合向量平行的坐标表示可得（x+4）y-（y-2）x=0，可求
（2）由
AC
⊥
BD
，可得
AC
•
BD
=0，结合（1）的关系式可求x，y，代入四边形的面积公式可求
解答：解（1）由题意得
AD
=
AB
+
BC
+
CD
=(x+4，y-2)，
BC
=(x，y)，…2分
因为
AD
∥
BC
，
所以（x+4）y-（y-2）x=0，即x+2y=0，①…4分
（2）由题意得
AC
=
AB
+
BC
=(x+6，y+1)，
BD
=
BC
+
CD
=(x-2，y-3)，…6分
因为
AC
⊥
BD
，
所以（x+6）（x-2）+（y+1）（y-3）=0，即x2+y2+4x-2y-15=0，②…8分
由①②得
x=2
y=-1
或
x=-6
y=3.
…10分
当
x=2
y=-1
时，
AC
=(8，0)，
BD
=(0，-4)，
则S四边形ABCD=
1
2
|
AC
||
BD
|=16…12分
当
x=-6
y=3
时，
AC
=(0，4)，
BD
=(-8，0)，
则S四边形ABCD=
1
2
|
AC
||
BD
|=16…14分
所以，四边形ABCD的面积为16
点评：本题主要考查了向量平行的坐标表示，向量数量积的性质的应用，属于基础试题．
练习册系列答案
相关题目
在平面直角坐标系xOy中，“方程
x2
k-1
+
y2
k-3
=1表示焦点在x轴上的双曲线”的充要条件是k∈
 
．
在平面直角坐标系xOy中，Pn（n，n2）（n∈N+）是抛物线y=x2上的点，△OPnPn+1的面积为Sn．
（1）求Sn；
（2）化简
1
S1
+
1
S2
+…+
1
Sn
；
（3）试证明S1+S2+…+Sn=
n(n+1)(n+2)
6
．
已知平面直角坐标系xOy中，A(4+2
3
，2)，B(4，4)，圆C是△OAB的外接圆．
（1）求圆C的方程；
（2）若过点（2，6）的直线l被圆C所截得的弦长为4
3
，求直线l的方程．
在平面直角坐标系xOy中，直线l的参数方程为：
x=-2+
3
5
t
y=2+
4
5
t
（t为参数），它与曲线C：（y-2）2-x2=1交于A，B两点．
（1）求|AB|的长；
（2）在以O为极点，x轴的正半轴为极轴建立极坐标系，设点P的极坐标为(2
2
，
3π
4
)，求点P到线段AB中点M的距离．
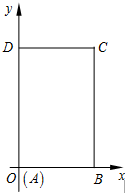精英家教网如图，在平面直角坐标系xOy中，已知矩形ABCD的两边AB，CD分别落在x轴、y轴的正半轴上，且AB=2，AD=4，点A与坐标原点重合．现将矩形折叠，使点A落在线段DC上，若折痕所在的直线的斜率为k，试写出折痕所在直线的方程及k的范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网