题目内容
设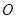
为坐标原点，抛物线
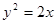与过焦点的直线交于
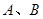两点，则
.
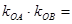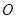为坐标原点，抛物线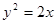与过焦点的直线交于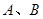两点，则 .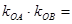
解：当直线与x轴不垂直时设直线l：y=k（x-1/ 2 ），
代入y2=2x，得：ky2-2y-1=0
设A（y 21 /2 ，y1），B（y 21 x2 / 2，y2）
∴y1•y2=-1
∴kOA•kOB=y1/ y 21 /2 •y2 /y 22 /2 ="4/" y1- y2 =-4
当直线与x轴垂直时，x="1-" 2 ，y=±1
∴kOA•kOB="1/1" /2 ×-1 /1 /2 =-4
故答案为-4
代入y2=2x，得：ky2-2y-1=0
设A（y 21 /2 ，y1），B（y 21 x2 / 2，y2）
∴y1•y2=-1
∴kOA•kOB=y1/ y 21 /2 •y2 /y 22 /2 ="4/" y1- y2 =-4
当直线与x轴垂直时，x="1-" 2 ，y=±1
∴kOA•kOB="1/1" /2 ×-1 /1 /2 =-4
故答案为-4
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的焦点
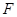与点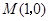
所得的线段与抛物线交于点
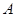，设点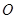
为坐标原点，则三角形
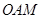的面积为（ ）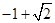
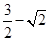
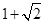
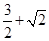
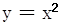和x轴、直线x=a(a>0)围成图形的面积为9，则a= 
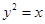的准线方程为 ；此抛物线的焦点是
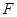，则经过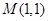
，且与准线相切的圆共有 个．
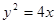上与焦点的距离等于5的点的横坐标是 ( )
（
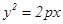）的焦点为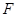
，
为坐标原点，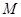
为抛物线上一点，且
,
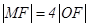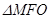的面积为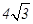
，则该抛物线的方程为 .
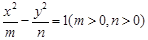的离心率为2，有一个焦点与抛物线
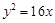的焦点重合，则
__________.
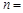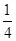
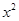的焦点坐标是______________．