题目内容
11.已知4男3女排队,每名男生至多与一名女生相邻,共有2304种不同的排法.分析 需要分三类,第一类,把4男生捆绑在一起,插入到3名女生排列所形成的4个空的1个空中,第二类,把4男生平均分为2组,分别插入到3名女生排列所形成的4个空的2个空中问题得以解决.第三类,把4男生分为(3,1)两组,把把1名男生插入到3名女生排列所形成的4个空的头或尾,把在一起的3个男生插入到剩下的3个空中的1个,根据分类计数原理即可解决.
解答 解:第一类,把4男生捆绑在一起,插入到3名女生排列所形成的4个空的1个空中,故有A44A33A41=576种,
第二类,把4男生平均分为2组,分别插入到3名女生排列所形成的4个空的2个空中,故有A42A33A42=864种,
第三类,把4男生分为(3,1)两组,把把1名男生插入到3名女生排列所形成的4个空的头或尾,把在一起的3个男生插入到剩下的3个空中的1个,
故有A21A41A33A33A31=864种,
根据分类计数原理得,576+864+864=2304
故答案为:2304.
点评 本题考查了排列组合的中的站队问题,本题采用间接法,属于中档题.

练习册系列答案
相关题目
2.等比数列{an}的首项为1,公比为q,前n项和记为S,由原数列各项的倒数组成一个新数列{$\frac{1}{{a}_{n}}$},则{$\frac{1}{{a}_{n}}$}的前n项之和S′是( )
| A. | $\frac{1}{S}$ | B. | $\frac{1}{{q}^{n}S}$ | C. | $\frac{{q}^{n}}{S}$ | D. | $\frac{S}{{q}^{n-1}}$ |
3.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≤0}\\{x-y+1≥0}\\{x+y-3≤0}\end{array}\right.$,则z=$\frac{x}{2}$+y的最大值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
20.以下是某个几何体的三视图(单位:cm),则该几何体的体积是( )
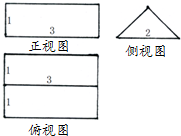

| A. | 2cm3 | B. | 3cm3 | C. | 4cm3 | D. | 5cm3 |
1.已知i是虚数单位,则复数z=i2015的虚部是( )
| A. | 0 | B. | -1 | C. | 1 | D. | -i |