题目内容
如图1-3-14,已知△ABC中,DE∥FG∥BC,AD∶DF∶FB =2∶3∶4,求S△ADE∶S四边形DEGF∶S四边形BCGF.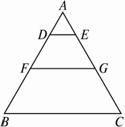
图1-3-14
思路分析:要求题目中的三部分的面积比,必须先求出△ADE、△AFG和△ABC的面积,才能求出两个四边形的面积.由已知DE∥FG∥BC的条件,可以得到相似三角形,再由相似三角形的面积比等于相似比的平方的性质,可求出相似三角形的面积比.题目中未给出具体数值,故应引入参数.
解:∵AD∶DF∶FB =2∶3∶4,?
设AD =2k,DF =3k,FB =4k(k>0),则AF =5k,AB =9k.?
∵DE∥FG,∴△ADE∽△AFG.?
∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() .?
.?
同理,可得![]() =(
=(![]() )2=
)2=![]() .
.
设S△ADE =4a,则S△AFG?=25a,S△ABC =81a(a>0).?
∴S四边形DEGF =25a - 4a =21a,?
S四边形BCGF?=81a - 25a = 56a.?
∴S△ADE∶S四边形DEGF∶S四边形BCGF=4∶21∶56.

练习册系列答案
相关题目
 (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.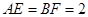 ,
,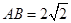 ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使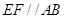 且
且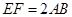 ,得一简单组合体
,得一简单组合体 如图2示,已知
如图2示,已知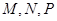 分别为
分别为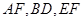 的中点.
的中点.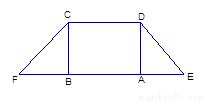
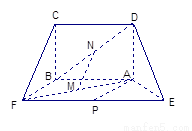
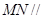 平面
平面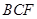 ;
;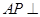
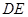 ;
; 多长时,平面
多长时,平面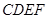 与平面
与平面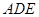 所成的锐二面角为
所成的锐二面角为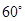 ?
?