题目内容
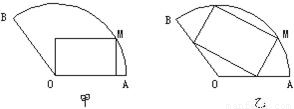
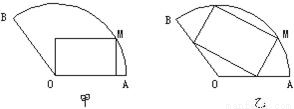
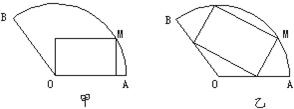 将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
分析:对甲种裁法分析设∠MOA=θ,则矩形的一边为20sinθ,一边为20cosθ,则得出面积,利用正弦函数取最值的方法求出最大面积;对乙种裁法分析设∠MOA=α利用三角函数表示出长为40sin(60°-α),再用相似三角形求得宽,进而表示出面积,利用余弦函数取最大值的方法求出最大面积.比较看哪个面积大即可.
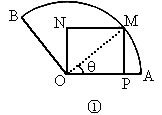
解答:解:对图甲,设∠MOA=θ,则S1=200sin2θ.
∴当θ=45°时,(S1)max=200cm2.
对图乙,设∠MOA=α,
则S2=
[cos(2α-60°)-cos60°].
当α=30°时,(S2)max=
cm2.
∵
>200,
∴用乙种方法好.
∴当θ=45°时,(S1)max=200cm2.
对图乙,设∠MOA=α,
则S2=
800
| ||
| 3 |
当α=30°时,(S2)max=
400
| ||
| 3 |
∵
400
| ||
| 3 |
∴用乙种方法好.
点评:考查学生根据实际问题选择函数类型的能力,以及运用两角和与差的正弦函数的能力,求正弦函数最值的能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
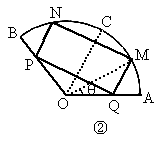
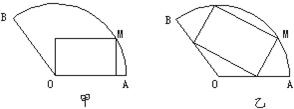 将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.