Question

已知椭圆和圆，且圆C与x轴交于A₁，A₂两点

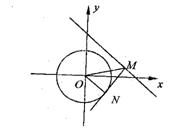
   （1）设椭圆C₁的右焦点为F，点P的圆C上异于A₁，A₂的动点，过原点O作直线PF的垂线交椭圆的右准线交于点Q，试判断直线PQ与圆C的位置关系，并给出证明。

   （2）设点在直线上，若存在点，使得（O为坐标原点），求的取值范围。来源:学+科+网Z+X+X+K]

Answer 1

直线P与圆C相切[来，

解析:

解：（1）直线P与圆C相切。……………………1分

证明如下：易得椭圆C₁的右焦点为，右准线为…………2分

设点则有，

又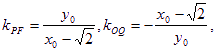

∴直线PQ的方程为

令，

即

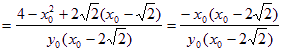
又…………………………5分

于是有，故OP⊥PQ，

直线P与圆C相切[来源:Zxxk.Com]

（3）如图，设，则，

即，即，而ON=2，

又由

于是有………………2分

整理，得

解得

的取值范围是