题目内容
 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=AC=2,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=AC=2,点E是PD的中点.(1)求证:AC⊥PB;
(2)求证:PB∥平面AEC;
(3)求三棱锥P-AEC的体积.
分析:(1)欲证AC⊥PB,只需证明AC⊥平面PAB,而AB⊥AC,易证PA⊥AC,问题即可解决;
(2)连接BD交AC于O,连接EO,证明EO∥PB,利用线面平行的判定定理即可得结论;
(3)通过体积轮换顶点公式即可求得三棱锥P-AEC的体积.
(2)连接BD交AC于O,连接EO,证明EO∥PB,利用线面平行的判定定理即可得结论;
(3)通过体积轮换顶点公式即可求得三棱锥P-AEC的体积.
解答: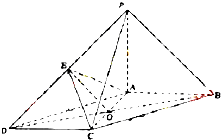 (1)证明:∵PA⊥平面ABCD,AC?平面ABCD,
(1)证明:∵PA⊥平面ABCD,AC?平面ABCD,
∴PA⊥AC …(2分)
又∵AB⊥AC,PA∩AB=A …(4分)
∴AC⊥平面PAB,又PB?平面PAB,
∴AC⊥PB …(6分)
(2)证明:连接BD交AC于O,连接EO.在△DPB中,E是PD的中点,
又O是BD的中点,∴EO∥PB.…(8分)
又EO?平面AEC,PB?平面AEC,
∴PB∥平面AEC.…(10分)
(3)∵VP-AEC=VC-PAE=VC-ADE=VE-ADC=
VP-ADC
∵VP-ADC=
×
×2×2×2=
∴
VP-ADC=
…(14分)
 (1)证明:∵PA⊥平面ABCD,AC?平面ABCD,
(1)证明:∵PA⊥平面ABCD,AC?平面ABCD,∴PA⊥AC …(2分)
又∵AB⊥AC,PA∩AB=A …(4分)
∴AC⊥平面PAB,又PB?平面PAB,
∴AC⊥PB …(6分)
(2)证明:连接BD交AC于O,连接EO.在△DPB中,E是PD的中点,
又O是BD的中点,∴EO∥PB.…(8分)
又EO?平面AEC,PB?平面AEC,
∴PB∥平面AEC.…(10分)
(3)∵VP-AEC=VC-PAE=VC-ADE=VE-ADC=
| 1 |
| 2 |
∵VP-ADC=
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查直线与平面垂直的性质与直线与平面平行的判定,关键在于熟练掌握平面垂直的性质与直线与平面平行的判定定理及其应用,属于中档题.

练习册系列答案
相关题目
 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点. 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°.
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°. 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°.
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°.