题目内容
函数y=ex(e为自然对数的底数)的图象向下平移b(0<b,b≠1)个单位后得到的图象记为Cb,Cb与x轴交于Ab点,与y轴交于Bb点,O为坐标原点
(1)写出Cb的解析式和Ab,Bb两点的坐标
(2)判断线段OAb,OBb长度大小,并证明你的结论
(3)是否存在两个互不相等且都不等于1的正实数m,n,使得Rt△OAmBm与Rt△OAnBn相似,如果相似,能否全等?证明你的结论.
解:(1)由题得y=ex-b,
令y=0,Ab(lnb,0);
令x=0,Bb(0,1-b).
(2)OAb=|lnb|,OBb=|1-b|.
①当0<b<1时,OAb=-lnb,OBb=1-b.
设函数f(x)-lnx-x-1 (0<x<1),
f'(x)= -1>0,
-1>0,
∴f(x)在(0,1)上单调递增,
∴f(x)<f(1)=0,
∴-lnx>-x+1
∴OAb>OBb.
②当b>1时,同理可得OAb>OBb,
(3)①当三角形同在第二象限时,0<m<1,0<n<1时,OAb>OBb,
若Rt△OAmBm与Rt△OAnBn相似,只有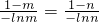 ?
?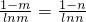 ,
,
设函数g(x)=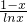 (0<x<1),
(0<x<1),
g'(x)=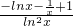 =
=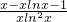 (0<x<1),
(0<x<1),
设函数h(x)=x-lnx-1,h'(x)=-lnx>0在(0,1)上恒成立,
∴h(x)在(0,1)上单调递增,∴h(x)<h(1)=0在(0,1)上恒成立,
∴g'(x)<0在(0,1)上恒成立,g(x)在(0,1)上单调递减,
所以当0<m<1,0<n<1时,不存在.当三角形同在第四象限时,m>1,n>1,同理可得m,n不存在.
③当三角形在不同象限时,不妨设0<m<1,n>1时,若Rt△OAmBm与Rt△OAnBn相似,
则OAm>OBm,OAn<OBn,则有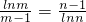 ,
,
设M={f1m|f1m=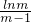 (0<m<1)},N={f2(n)|f2(n)=
(0<m<1)},N={f2(n)|f2(n)=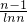 (n>1)},
(n>1)},
有g(x)性质可得:取m∈(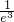 ,
, ),f1(m)=
),f1(m)=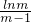 在(
在(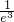 ,
, )上单调递增,
)上单调递增,
∴f1(m)∈[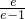 ,
,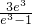 ],2∈[
],2∈[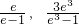 ]
]
取n∈[e,e2],f2(n)=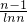 在[e,e2]递增,
在[e,e2]递增,
∴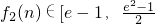 ],2∈[e-1,
],2∈[e-1,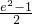 ].
].
可得M∩N≠φ,因此存在0<m<1,n>1,使得Rt△OAmBm与Rt△OAnBn相似.
如果全等,则有.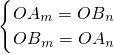 ?
?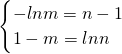 ?
?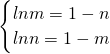 .
.
由lnm=1-n?m=e1-n,代入lnn=1-m,
lnn=1-e1-n?enlnn=en-e.
设函数F(x)=exlnx-ex+e (x>1),
F'(x)=exlnx+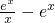 =
=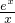 (xlnx-x+1).
(xlnx-x+1).
设函数H(x)=xlnx-x+1 ( x>1),
H'(x)=lnx+1-1=lnx>0,
所以H(x)在(1,+∞)上单调递增,∴H(x)>H(1)=0.
所以F'(x)>0在(1,+∞)上恒成立,F(x)在(1,+∞)上单调递增
∴F(x)>F(1)=0.
因此不存在n>1,使得enlnn=en-e.
所以不存在两个互不相等且都不等于1的正实数m,n,使得Rt△OAmBm与Rt△OAnBn全等.
分析:(1)直接利用图象的平移规律即可求Cb的解析式,再令y=0以及x=0即可求出Ab,Bb两点的坐标
(2)先求出线段OAb,OBb长的表达式,分b的取值并借助于函数的单调性来比较其长度大小即可.
(3)先对两个三角形所在象限分情况讨论,根据相似得到的结论求出正实数m,n的范围,看是否符合要求即可.
点评:本题综合考查指数函数的性质以及函数图象的变换和三角形相似及全等对应的结论,是对知识的综合考查,属于难题.
令y=0,Ab(lnb,0);
令x=0,Bb(0,1-b).
(2)OAb=|lnb|,OBb=|1-b|.
①当0<b<1时,OAb=-lnb,OBb=1-b.
设函数f(x)-lnx-x-1 (0<x<1),
f'(x)=
 -1>0,
-1>0,∴f(x)在(0,1)上单调递增,
∴f(x)<f(1)=0,
∴-lnx>-x+1
∴OAb>OBb.
②当b>1时,同理可得OAb>OBb,
(3)①当三角形同在第二象限时,0<m<1,0<n<1时,OAb>OBb,
若Rt△OAmBm与Rt△OAnBn相似,只有
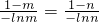 ?
?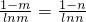 ,
,设函数g(x)=
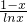 (0<x<1),
(0<x<1),g'(x)=
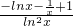 =
=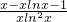 (0<x<1),
(0<x<1),设函数h(x)=x-lnx-1,h'(x)=-lnx>0在(0,1)上恒成立,
∴h(x)在(0,1)上单调递增,∴h(x)<h(1)=0在(0,1)上恒成立,
∴g'(x)<0在(0,1)上恒成立,g(x)在(0,1)上单调递减,
所以当0<m<1,0<n<1时,不存在.当三角形同在第四象限时,m>1,n>1,同理可得m,n不存在.
③当三角形在不同象限时,不妨设0<m<1,n>1时,若Rt△OAmBm与Rt△OAnBn相似,
则OAm>OBm,OAn<OBn,则有
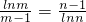 ,
,设M={f1m|f1m=
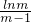 (0<m<1)},N={f2(n)|f2(n)=
(0<m<1)},N={f2(n)|f2(n)=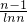 (n>1)},
(n>1)},有g(x)性质可得:取m∈(
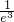 ,
, ),f1(m)=
),f1(m)=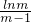 在(
在(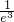 ,
, )上单调递增,
)上单调递增,∴f1(m)∈[
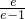 ,
,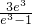 ],2∈[
],2∈[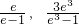 ]
]取n∈[e,e2],f2(n)=
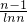 在[e,e2]递增,
在[e,e2]递增,∴
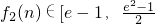 ],2∈[e-1,
],2∈[e-1,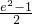 ].
].可得M∩N≠φ,因此存在0<m<1,n>1,使得Rt△OAmBm与Rt△OAnBn相似.
如果全等,则有.
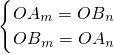 ?
?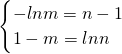 ?
?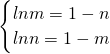 .
.由lnm=1-n?m=e1-n,代入lnn=1-m,
lnn=1-e1-n?enlnn=en-e.
设函数F(x)=exlnx-ex+e (x>1),
F'(x)=exlnx+
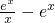 =
=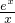 (xlnx-x+1).
(xlnx-x+1).设函数H(x)=xlnx-x+1 ( x>1),
H'(x)=lnx+1-1=lnx>0,
所以H(x)在(1,+∞)上单调递增,∴H(x)>H(1)=0.
所以F'(x)>0在(1,+∞)上恒成立,F(x)在(1,+∞)上单调递增
∴F(x)>F(1)=0.
因此不存在n>1,使得enlnn=en-e.
所以不存在两个互不相等且都不等于1的正实数m,n,使得Rt△OAmBm与Rt△OAnBn全等.
分析:(1)直接利用图象的平移规律即可求Cb的解析式,再令y=0以及x=0即可求出Ab,Bb两点的坐标
(2)先求出线段OAb,OBb长的表达式,分b的取值并借助于函数的单调性来比较其长度大小即可.
(3)先对两个三角形所在象限分情况讨论,根据相似得到的结论求出正实数m,n的范围,看是否符合要求即可.
点评:本题综合考查指数函数的性质以及函数图象的变换和三角形相似及全等对应的结论,是对知识的综合考查,属于难题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目