题目内容
“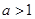 ”是“
”是“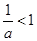 ”成立的 ( )
”成立的 ( )
A 充分不必要条件 B 必要不充分条件
C 充分必要条件 D 既非充分也非必要条件
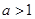 ”是“
”是“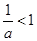 ”成立的 ( )
”成立的 ( ) A 充分不必要条件 B 必要不充分条件
C 充分必要条件 D 既非充分也非必要条件
A
可以把不等式“ <1”变形解出a的取值范围来,然后再作判断,具体地来说,两边同乘以分母a要分类讨论,分a>0,a<0两类来讨论,除了用符号法则,这是解答分式不等式的另一种重要方法.
<1”变形解出a的取值范围来,然后再作判断,具体地来说,两边同乘以分母a要分类讨论,分a>0,a<0两类来讨论,除了用符号法则,这是解答分式不等式的另一种重要方法.
解:由 <1得:
<1得:
当a>0时,有1<a,即a>1;
当a<0时,不等式恒成立.
所以 <1?a>1或a<0
<1?a>1或a<0
从而a>1是 <1的充分不必要条件.
<1的充分不必要条件.
故应选:A
考查不等式的性质及其应用,解分式不等式的问题,不等式的等价变形!本题需要注意的是在利用不等式的乘法单调性时易出错,比如本题中若原不等式两边同乘以a,等到a>1就是对不等式两边同乘以一个正数还是负数不等式是否改变方向认识不足导致的错误.
 <1”变形解出a的取值范围来,然后再作判断,具体地来说,两边同乘以分母a要分类讨论,分a>0,a<0两类来讨论,除了用符号法则,这是解答分式不等式的另一种重要方法.
<1”变形解出a的取值范围来,然后再作判断,具体地来说,两边同乘以分母a要分类讨论,分a>0,a<0两类来讨论,除了用符号法则,这是解答分式不等式的另一种重要方法.解:由
 <1得:
<1得:当a>0时,有1<a,即a>1;
当a<0时,不等式恒成立.
所以
 <1?a>1或a<0
<1?a>1或a<0从而a>1是
 <1的充分不必要条件.
<1的充分不必要条件.故应选:A
考查不等式的性质及其应用,解分式不等式的问题,不等式的等价变形!本题需要注意的是在利用不等式的乘法单调性时易出错,比如本题中若原不等式两边同乘以a,等到a>1就是对不等式两边同乘以一个正数还是负数不等式是否改变方向认识不足导致的错误.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
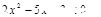 的一个必要不充分条件是( ).
的一个必要不充分条件是( ).



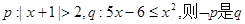 的
的 ,条件
,条件 ,则
,则 是
是 的( )
的( )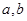 是实数,则“
是实数,则“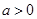 且
且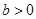 ”是“
”是“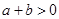 且
且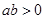 ”的 ( )
”的 ( ) 成立的一个必要不充分条件是( )
成立的一个必要不充分条件是( )


 ,或
,或
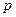 :实数
:实数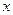 满足
满足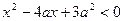 ,其中
,其中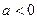 ;
;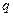 :实数
:实数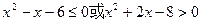 ,且
,且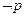 是
是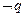 的必要不充分条件,求
的必要不充分条件,求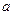 的取值范围。
的取值范围。 ”是“对任意的正数x,
”是“对任意的正数x, ”的
”的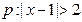 ,条件
,条件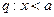 ,且
,且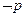 是
是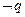 的充分不必要条件,则a的取值范围是 ( )
的充分不必要条件,则a的取值范围是 ( ) 


