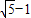题目内容
设集合M和N为平面中的两个点集，若存在点A∈M、B∈N，使得对任意的点A∈M、B∈N，均有|AB|≥|AB|，则称|AB|为点集M和N的距离，记为d（M，N）=|AB|．已知集合M={（x，y）|x2+（y-2）2≤1}，N={（x，y）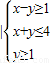
}，则d（M，N）=（ ）A．
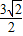
B．
C．
D．
【答案】分析：先画出集合M，N表示的平面图形，欲求点集M和N的距离，即求出两图形中相距最近的两点间的距离即可．故先求出圆的圆心与半径，利用圆心到A点的距离即可求出满足题意的距离．
解答：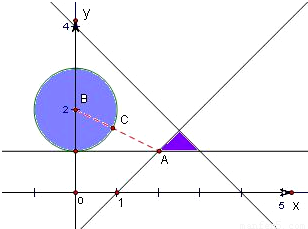
解：集合M={（x，y）|x2+（y-2）2≤1}表示的图形是圆及内部，N={（x，y）
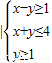}表示一个三角形，如图所示，
M和N的距离即为两图形中相距最近的两点间的距离．
由于圆心B（0，2）到点A（2，1）的距离为：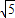
，
∴则d（M，N）=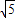
-1；
故选D．
点评：本题是基础题，考查简单线性规划的应用，直线与圆的位置关系，点到点的距离，考查计算能力．
解答：
解：集合M={（x，y）|x2+（y-2）2≤1}表示的图形是圆及内部，N={（x，y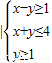）}表示一个三角形，如图所示，M和N的距离即为两图形中相距最近的两点间的距离．
由于圆心B（0，2）到点A（2，1）的距离为：
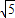，∴则d（M，N）=
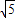-1；故选D．
点评：本题是基础题，考查简单线性规划的应用，直线与圆的位置关系，点到点的距离，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
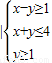}，则d（M，N）=（ ）
