题目内容
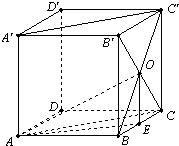
 如图,正方体的棱长为1,B′C∩BC′=O,求:
如图,正方体的棱长为1,B′C∩BC′=O,求:(1)AO与A′C′所成角;
(2)AO与平面ABCD所成角的正切值;
(3)平面AOB与平面AOC所成角.
分析:(1)根据A′C′∥AC,可得AO与A′C′所成角就是∠OAC,解Rt△AOC,求出∠OAC的大小.
(2)如图,作OE⊥BC于E,连接AE,由平面BC′⊥平面ABCD,得OE⊥平面ABCD,∠OAE为OA与平面ABCD所成角,解在Rt△OAE,求出tan∠OAE的大小.
(3)由OC⊥OA,OC⊥OB,可知OC⊥平面AOB,又OC?平面AOC,故平面AOB⊥平面AOC,从而得到平面AOB与平面AOC所成角为90°.
(2)如图,作OE⊥BC于E,连接AE,由平面BC′⊥平面ABCD,得OE⊥平面ABCD,∠OAE为OA与平面ABCD所成角,解在Rt△OAE,求出tan∠OAE的大小.
(3)由OC⊥OA,OC⊥OB,可知OC⊥平面AOB,又OC?平面AOC,故平面AOB⊥平面AOC,从而得到平面AOB与平面AOC所成角为90°.
解答:解:(1)∵A′C′∥AC,∴AO与A′C′所成角就是∠OAC.∵OC⊥OB,AB⊥平面BC′,∴OC⊥OA,
在Rt△AOC中,OC═OC=
,AC=
,∴∠OAC=30°.(4分)
(2)如图,作OE⊥BC于E,连接AE,∵平面BC′⊥平面ABCD,∴OE⊥平面ABCD,∠OAE为OA与平面ABCD所成角.
在Rt△OAE中,OE=
,AE=
=
,∴tan∠OAE=
=
.(9分)
(3)∵OC⊥OA,OC⊥OB,∴OC⊥平面AOB.又∵OC?平面AOC,∴平面AOB⊥平面AOC,即平面AOB与平面AOC所成角为90°.(13分)
在Rt△AOC中,OC═OC=
| ||
| 2 |
| 2 |
(2)如图,作OE⊥BC于E,连接AE,∵平面BC′⊥平面ABCD,∴OE⊥平面ABCD,∠OAE为OA与平面ABCD所成角.
在Rt△OAE中,OE=
| 1 |
| 2 |
12+(
|
| ||
| 2 |
| OE |
| AE |
| ||
| 5 |
(3)∵OC⊥OA,OC⊥OB,∴OC⊥平面AOB.又∵OC?平面AOC,∴平面AOB⊥平面AOC,即平面AOB与平面AOC所成角为90°.(13分)

点评:本题主要考查异面直线所成的角的定义和求法,求直线和平面所成的角,求二面角的大小的方法,找出这些角,是解题的关键.

练习册系列答案
相关题目
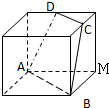 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是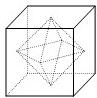 如图,正方体的棱长为a,将正方体的六个面的中心连接起来,构成一个八面体,这个八面体的体积是
如图,正方体的棱长为a,将正方体的六个面的中心连接起来,构成一个八面体,这个八面体的体积是
 如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=
如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF= 的棱长为
的棱长为 ,点
,点 在棱
在棱 上,
上, ,点
,点 是平面
是平面 上的动点,且动点
上的动点,且动点
