题目内容
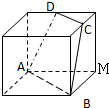 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是分析:分别取AB、CD的中点E、F,连EF,过M作MN⊥EF于N,则MN的长为点M到截面ABCD的距离.在△CAM中计算tan∠CAM.进而求得sin∠CAM,进而在△MFN中计算MN=MFsin∠CAM求得答案.
解答: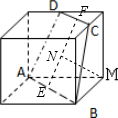 解:分别取AB、CD的中点E、F连EF,过M作MN⊥EF于N,则MN的长为点M到截面ABCD的距离.
解:分别取AB、CD的中点E、F连EF,过M作MN⊥EF于N,则MN的长为点M到截面ABCD的距离.
现在△CAM中计算tan∠CAM=2
,
∴sin∠CAM=
,
再在△MFN中计算MN=MFsin∠CAM=
.
故答案为
 解:分别取AB、CD的中点E、F连EF,过M作MN⊥EF于N,则MN的长为点M到截面ABCD的距离.
解:分别取AB、CD的中点E、F连EF,过M作MN⊥EF于N,则MN的长为点M到截面ABCD的距离.现在△CAM中计算tan∠CAM=2
| 2 |
∴sin∠CAM=
2
| ||
| 3 |
再在△MFN中计算MN=MFsin∠CAM=
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
点评:本题主要考查了点、线、面间的距离计算.考查了学生对立体几何知识的理解和运用.

练习册系列答案
相关题目
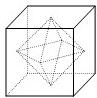 如图,正方体的棱长为a,将正方体的六个面的中心连接起来,构成一个八面体,这个八面体的体积是
如图,正方体的棱长为a,将正方体的六个面的中心连接起来,构成一个八面体,这个八面体的体积是
 如图,正方体的棱长为1,B′C∩BC′=O,求:
如图,正方体的棱长为1,B′C∩BC′=O,求: 如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=
如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF= 的棱长为
的棱长为 ,点
,点 在棱
在棱 上,
上, ,点
,点 是平面
是平面 上的动点,且动点
上的动点,且动点
