题目内容
5.比较大小:(1)tan$\frac{2π}{7}$与tan$\frac{10π}{7}$;
(2)tan$\frac{6π}{5}$与tan(-$\frac{13π}{5}$)
分析 (1)用诱导公式得出tan$\frac{10π}{7}$=$tan\frac{3π}{7}$;利用单位圆中的正切线表示得出AT1为$\frac{2π}{7}$的正切线,AT2为$\frac{3π}{7}$的正切线,比较大小即可.
(2)tan$\frac{6π}{5}$=tan$\frac{π}{5}$,tan(-$\frac{13π}{5}$)=tan$\frac{2π}{5}$,利用单位圆中的正切线比较大小.
解答 解:(1)tan$\frac{2π}{7}$,tan$\frac{10π}{7}$=$tan\frac{3π}{7}$;
根据单位圆中的正切线表示得出AT1为$\frac{2π}{7}$的正切线,
AT2为$\frac{3π}{7}$的正切线,
可知:AT2>AT1,
∴tan$\frac{2π}{7}$<tan$\frac{10π}{7}$;
(2)tan$\frac{6π}{5}$=tan$\frac{π}{5}$,tan(-$\frac{13π}{5}$)=tan$\frac{2π}{5}$,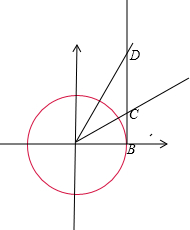
根据单位圆中的正切线表示得出BC为$\frac{π}{5}$的正切线,
BD为$\frac{2π}{5}$的正切线,
可知:BD>BC,
∴tan$\frac{π}{5}$<tan$\frac{2π}{5}$;
即tan$\frac{6π}{5}$∠tan(-$\frac{13π}{5}$)
点评 本题考察了诱导公式的化简运用,正切线的画法,属于三角函数线的基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,直线x=$\frac{{a}^{2}}{c}$与一条渐近线交于点A,△OAF的面积为$\frac{{a}^{2}}{2}$(O为原点),则两条渐近线的夹角为( )
| A. | 30° | B. | 45° | C. | 90° | D. | 60° |
20.函数f(x)=$\frac{lnx}{x}$(x>0)( )
| A. | 在(0,+∞)上是减函数 | |
| B. | 在(0,+∞)上是减函数 | |
| C. | 在(0,e)上是增函数,在(e,+∞)上是减函数 | |
| D. | 在(0,e)上是减函数,在(e,+∞)上是增函数 |
15.用秦九韶算法计算多项式f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值 时,v3的值( )
| A. | -10 | B. | -80 | C. | 40 | D. | 80 |