题目内容
若直线l：x=my+n（n＞0）过点A（4，4
），若可行域
的外接圆的面积为
，则实数n的值为（ ）
| 3 |
|
| 64π |
| 3 |
| A、8 | B、7 | C、6 | D、9 |
分析：由直线l：x=my+n（n＞0）和直线
x-y=0均过点A（4，4
）作出可行域，由三角形外接圆的面积求出外接圆的半径，由正弦定理求得|AB|，然后由两点间的距离公式求得n的值．
| 3 |
| 3 |
解答：解：设l：x=my+n（n＞0）与x轴的交点为B（n，0），
∵直线l：x=my+n（n＞0）过点A（4，4
），
x-y=0也过点A（4，4
），
∴直线l：x=my+n（n＞0）经过一、二、四象限，∴m＜0．
∴可行域为△OAB，且∠AOB=60°，如图，
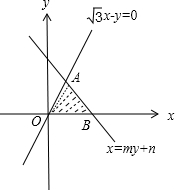
∵可行域
的外接圆的面积为
，
∴△OAB外接圆的直径为
．
由正弦定理得：
=2R=
，
∴AB=
×
=8．
由两点间的距离公式得：
=8，
解得：n=0（舍）或n=8．
故选：A．
∵直线l：x=my+n（n＞0）过点A（4，4
| 3 |
| 3 |
| 3 |
∴直线l：x=my+n（n＞0）经过一、二、四象限，∴m＜0．
∴可行域为△OAB，且∠AOB=60°，如图，
∵可行域
|
| 64π |
| 3 |
∴△OAB外接圆的直径为
16
| ||
| 3 |
由正弦定理得：
| AB |
| sin60° |
16
| ||
| 3 |
∴AB=
16
| ||
| 3 |
| ||
| 2 |
由两点间的距离公式得：
(4-n)2+(4
|
解得：n=0（舍）或n=8．
故选：A．
点评：本题考查了二元一次不等式的几何意义，是简单的线性规划问题，解答的关键是正确作出可行域，考查了正弦定理在解三角形中的应用，是中档题．
练习册系列答案
一线名师提优试卷系列答案
相关题目