题目内容
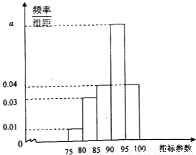 针对频繁发生的校车事故,2011年12月27日,工信部发布公告,公开征求对新制订的有关校车安全的几个条例的意见,我市为了了解实际情况,随机抽取了 100辆校车进行检测,将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图.
针对频繁发生的校车事故,2011年12月27日,工信部发布公告,公开征求对新制订的有关校车安全的几个条例的意见,我市为了了解实际情况,随机抽取了 100辆校车进行检测,将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图.(1)由图中数据,求a的值;
(2)若要从指标参数在[85,90)、[90,95)、[95,100]的三组校车中,用分层抽样方法抽取8辆,作另一项指标脚定,求各组分别抽取的车辆数;
(3)某学校根据自己的实际情况,从(2)中抽取的8辆校车中再随机选4辆来考察校车的价格,设指标参数在[90,95)内的校车被选取的辆数为ξ,求ξ的分布列以及ξ的数学期望.
【答案】分析:(1)由频率分布直方图知,组距为5,由此能求出a.
(2)先求出指标参数在[85,90],[90,95],[95,100]的车辆数,再计算在[85,90],[90,95],[95,100]三组中分别抽取的车辆数.
(3)设指标参数在[90,95]内的车辆被抽取的数量为随机变量ξ,则ξ=0,1,2,3,4,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),P(ξ=4),由此能求出ξ的分布列以及ξ的数学期望.
解答:解:(1)由频率分布直方图知,组距为5,
∴(a+0.04+0.04+0.03+0.01)×5=1,
解得a=0.08.
(2)指标参数在[85,90],[90,95],[95,100]的车辆数分别为
0.04×5×100=20,
0.08×5×100=40,
0.04×5×100=20,
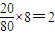 ,
,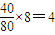 ,
,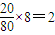 ,
,
∴在[85,90],[90,95],[95,100]三组中分别抽取2辆,4辆,2辆.
(3)设指标参数在[90,95]内的车辆被抽取的数量为随机变量ξ,
则ξ=0,1,2,3,4,
且P(ξ=0)=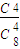 =
=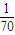 ,P(ξ=1)=
,P(ξ=1)=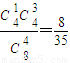 ,
,
P(ξ=2)=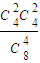 =
=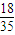 ,P(ξ=3)=
,P(ξ=3)=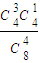 =
= ,P(ξ=4)=
,P(ξ=4)=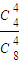 =
=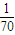 ,
,
∴ξ的分布列为:
∴Eξ=0×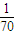 +1×
+1×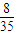 +2×
+2×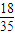 +3×
+3×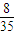 +4×
+4×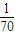 =2.
=2.
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是利用独立重复试验的概率公式做出概率的值,本题是一个中档题目.
(2)先求出指标参数在[85,90],[90,95],[95,100]的车辆数,再计算在[85,90],[90,95],[95,100]三组中分别抽取的车辆数.
(3)设指标参数在[90,95]内的车辆被抽取的数量为随机变量ξ,则ξ=0,1,2,3,4,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),P(ξ=4),由此能求出ξ的分布列以及ξ的数学期望.
解答:解:(1)由频率分布直方图知,组距为5,
∴(a+0.04+0.04+0.03+0.01)×5=1,
解得a=0.08.
(2)指标参数在[85,90],[90,95],[95,100]的车辆数分别为
0.04×5×100=20,
0.08×5×100=40,
0.04×5×100=20,
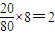 ,
,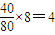 ,
,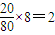 ,
,∴在[85,90],[90,95],[95,100]三组中分别抽取2辆,4辆,2辆.
(3)设指标参数在[90,95]内的车辆被抽取的数量为随机变量ξ,
则ξ=0,1,2,3,4,
且P(ξ=0)=
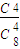 =
=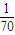 ,P(ξ=1)=
,P(ξ=1)=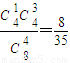 ,
,P(ξ=2)=
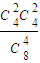 =
=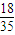 ,P(ξ=3)=
,P(ξ=3)=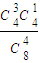 =
= ,P(ξ=4)=
,P(ξ=4)=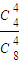 =
=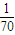 ,
,∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 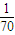 | 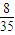 | 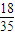 | 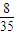 | 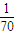 |
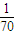 +1×
+1×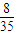 +2×
+2×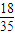 +3×
+3×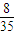 +4×
+4×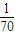 =2.
=2.点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是利用独立重复试验的概率公式做出概率的值,本题是一个中档题目.

练习册系列答案
相关题目
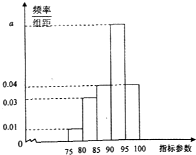 (2012•衡阳模拟)针对频繁发生的校车事故,2011年12月27日,工信部发布公告,公开征求对新制订的有关校车安全的几个条例的意见,我市为了了解实际情况,随机抽取了 100辆校车进行检测,将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图.
(2012•衡阳模拟)针对频繁发生的校车事故,2011年12月27日,工信部发布公告,公开征求对新制订的有关校车安全的几个条例的意见,我市为了了解实际情况,随机抽取了 100辆校车进行检测,将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图.