Question

针对近期频繁出现的校车事故，国家决定制定校车标准以保障幼儿园儿童的人生安全，已知某大型公办幼儿园计划用350万元购买A型和B型两款车投入运营，购买总量不超过15辆，其中购买A型校车需25万元/辆，购买B型校车需20万元/辆，假设A型校车的准坐最大人数为30人/辆，B型校车的准坐最大人数为25人/辆，那么为了使该校车所能接送的学生人数最多，则须安排购买（　　）

A．10辆A型校车，5辆B型校车

B．9辆A型校车，6辆B型校车

C．11辆A型校车，4辆B型校车

D．12辆A型校车，3辆B型校车

Answer 1

分析：设安排购买x辆A型校车，y辆B型校车（x，y∈N₊），则

25x+20y≤350 0＜x+y≤15

，目标函数z=30x+25y（x，y∈N₊），可行域为四边形OABC，由图可得，目标函数z=30x+25y（x，y∈N₊）的最大值，从而可得结论．

解答：解：设安排购买x辆A型校车，y辆B型校车（x，y∈N₊），则

25x+20y≤350 0＜x+y≤15

目标函数z=30x+25y（x，y∈N₊），可行域为四边形OABC，如图，

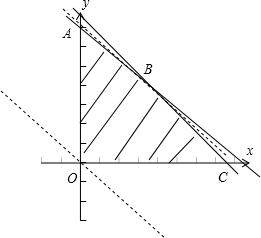
其中B点坐标由

25x+20y=350 x+y=15

可得，即B（10，5）
由图可得，目标函数z=30x+25y（x，y∈N₊）在B处取得最大值
故安排购买10辆A型校车，5辆B型校车
故选A．

点评：本题考查线性规划知识的运用，考查学生分析解决问题的能力，确定可行域与目标函数是关键．