题目内容
对于下列命题:①在△ABC中,若sin2A=sin2B,则△ABC为等腰三角形;
②已知a,b,c是△ABC的三边长,若a=2,b=5,
 ,则△ABC有两组解;
,则△ABC有两组解;③设
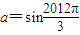 ,
,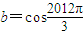 ,
,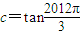 ,则a>b>c;
,则a>b>c;④将函数
 图象向左平移
图象向左平移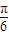 个单位,得到函数
个单位,得到函数 图象.
图象.其中正确命题的个数是( )
A.0
B.1
C.2
D.3
【答案】分析:可根据三角函数的性质与正弦定理对四个结论逐一进行判断,即可得到正确的结论
解答:解:①,∵△ABC中,若sin2A=sin2B,
∴2A=2B或2A+2B=π,
∴△ABC为等腰三角形或直角三角形,故①错误;
②,∵a,b,c是△ABC的三边长,若a=2,b=5,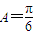 ,
,
∴由正弦定理得: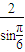 =
=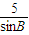 ,
,
∴sinB= ,这是不可能的,故②错误;
,这是不可能的,故②错误;
③,∵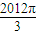 =335×2π+
=335×2π+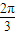 ,
,
∴a=sin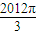 =sin
=sin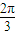 =
=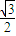 ,同理可得b=cos
,同理可得b=cos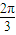 =-
=- ,c=tan
,c=tan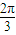 =-
=-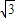 ,故a>b>c,于是③正确;
,故a>b>c,于是③正确;
④,将函数y=2sin(3x+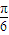 )图象向左平移
)图象向左平移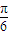 个单位,
个单位,
得:y=2sin[3(x+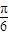 )+
)+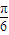 ]
]
=2sin[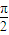 +(3x+
+(3x+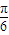 )]
)]
=2cos(3x+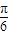 ),故④正确;
),故④正确;
故选C.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数和正弦定理,属于中档题.
解答:解:①,∵△ABC中,若sin2A=sin2B,
∴2A=2B或2A+2B=π,
∴△ABC为等腰三角形或直角三角形,故①错误;
②,∵a,b,c是△ABC的三边长,若a=2,b=5,
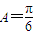 ,
,∴由正弦定理得:
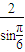 =
=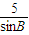 ,
,∴sinB=
 ,这是不可能的,故②错误;
,这是不可能的,故②错误;③,∵
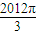 =335×2π+
=335×2π+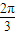 ,
,∴a=sin
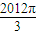 =sin
=sin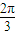 =
=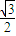 ,同理可得b=cos
,同理可得b=cos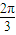 =-
=- ,c=tan
,c=tan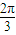 =-
=-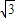 ,故a>b>c,于是③正确;
,故a>b>c,于是③正确;④,将函数y=2sin(3x+
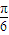 )图象向左平移
)图象向左平移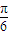 个单位,
个单位,得:y=2sin[3(x+
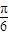 )+
)+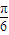 ]
]=2sin[
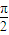 +(3x+
+(3x+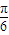 )]
)]=2cos(3x+
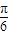 ),故④正确;
),故④正确;故选C.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数和正弦定理,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 (
( 为常数,且
为常数,且 ),对于下列命题:
),对于下列命题: 在每一点处都连续;
在每一点处都连续; ,则函数
,则函数 处可导;
处可导; ;
; ,恒有
,恒有 .
.
 (
( 为常数,且
为常数,且 ),对于下列命题:
),对于下列命题: 在每一点处都连续;
在每一点处都连续; ,则函数
,则函数 处可导;
处可导; ;
; ,恒有
,恒有 .
.