题目内容
某企业的某种产品产量与单位成本统计数据如下:
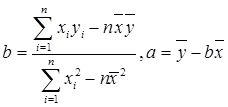
(用最小二乘法求线性回归方程系数公式
注: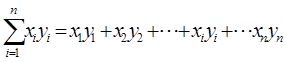 ,
,
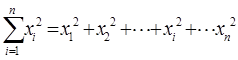 )
)
(1)试确定回归方程;
(2)指出产量每增加1 件时,单位成本下降多少?
(3)假定产量为6 件时,单位成本是多少?单位成本为70元/件时,产量应为多少件?
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量(千件) | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本(元/件) | 73 | 72 | 71 | 73 | 69 | 68 |
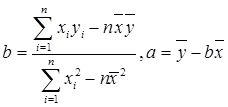
(用最小二乘法求线性回归方程系数公式
注:
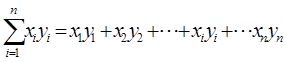 ,
,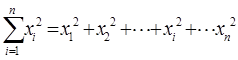 )
)(1)试确定回归方程;
(2)指出产量每增加1 件时,单位成本下降多少?
(3)假定产量为6 件时,单位成本是多少?单位成本为70元/件时,产量应为多少件?
(1) y=bx+a (2) 1.818元(3) 4 051件
本题考查线性回归方程和两组数据的平均数和方差的比较,本题是一个基础题,解题的关键在于运算,只要数字的运算不出错,题目就没有问题.
(1)做出横标和纵标的平均数,写出最小二乘法的表示式,代入求出的结果,得到线性回归方程的系数,再求出a的值,写出线性回归方程.
(2)产量每增加1 件时,单位成本下降1.818元
(3)当月产量为6千件时,即x=6,y=66.455,即当月产量6千件时,单位成本是66.455
解:(1)设x表示每月产量(单位:千件),y表示单位成本(单位:元/件),作散点图.由图知y与x间呈线性相关关系,设线性回归方程为y=bx+a.

由公式可求得b≈-1.818,a=77.364,∴回归方程为y=-1.818x+77.364.
(2)由回归方程知,每增加1 件产量,单位成本下降1.818元.
(3)当x=6时,y=-1.818×6+77.364=66.455;
当y=70时,70=-1.818x+77.364,得
x≈4. 051千件.
∴ 产量为6 件时,单位成本是66.455元/件,单位成本是70元/件时,产量约为4 051件.
(1)做出横标和纵标的平均数,写出最小二乘法的表示式,代入求出的结果,得到线性回归方程的系数,再求出a的值,写出线性回归方程.
(2)产量每增加1 件时,单位成本下降1.818元
(3)当月产量为6千件时,即x=6,y=66.455,即当月产量6千件时,单位成本是66.455
解:(1)设x表示每月产量(单位:千件),y表示单位成本(单位:元/件),作散点图.由图知y与x间呈线性相关关系,设线性回归方程为y=bx+a.

由公式可求得b≈-1.818,a=77.364,∴回归方程为y=-1.818x+77.364.
(2)由回归方程知,每增加1 件产量,单位成本下降1.818元.
(3)当x=6时,y=-1.818×6+77.364=66.455;
当y=70时,70=-1.818x+77.364,得
x≈4. 051千件.
∴ 产量为6 件时,单位成本是66.455元/件,单位成本是70元/件时,产量约为4 051件.

练习册系列答案
相关题目
 的男生有30人,女生4人;身高<170的男生有10人。
的男生有30人,女生4人;身高<170的男生有10人。 列联表:
列联表:

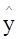 =1.23x+4
=1.23x+4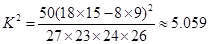 .
.
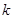
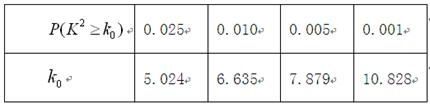
 的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”; 的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;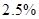 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;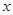 与
与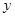 之间的几组数据如下表:
之间的几组数据如下表: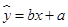 必过 ( )
必过 ( ) B.
B. C.
C. D.
D.
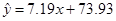 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
,据此可以预测这个孩子10岁时的身高,则正确的叙述是( ) 
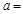 3
3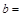
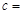
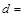 11
11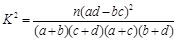 ,其中
,其中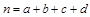 .)
.)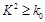 )
)