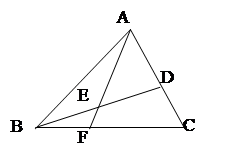
题目内容
已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF="CF=√2," AF:FB:BE=4:2:1,若CE与圆相切,则线段CE的长为______.
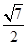
解析试题分析:设AF=4k,BF=2k,BE=k,由DF•FC=AF•BF,得2=8k2,即k= ∴AF=2,BF=1,BE=
∴AF=2,BF=1,BE= ,AE=
,AE=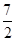 ,由切割定理得CE2=BE•EA=
,由切割定理得CE2=BE•EA= ×
×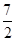 =
=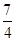
∴CE=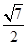 。故答案为
。故答案为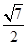
考点:本试题主要考查直线与圆的位置关系。
点评:解决该试题的关键是对于切割线定理的灵活运用,以及相交弦定理的运用,进而建立关系式得到。这也是几何中求解长度中常用的解题公式。

练习册系列答案
相关题目

 为⊙
为⊙ 的直径,
的直径,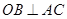 ,弦
,弦 交
交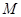 .若
.若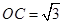 ,
,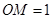 ,则
,则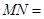 _____.
_____.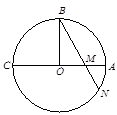
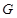 是△
是△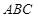 的外心,
的外心,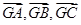 是三个单位向量,且2
是三个单位向量,且2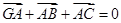 ,
,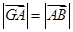 ,如图所示,△
,如图所示,△ 分别在
分别在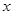 轴和
轴和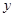 轴的非负半轴上移动,
轴的非负半轴上移动,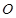 是坐标原点,则
是坐标原点,则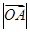 的最大值为 。
的最大值为 。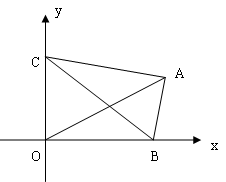
 圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是
圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是 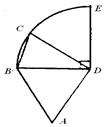
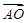 ·
·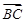 的值是
的值是 
 AB于D,CD=3cm,
AB于D,CD=3cm,
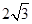 ,OA=
,OA= OM,求MN的长
OM,求MN的长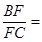 .
.