题目内容
已知实数
≤16,t满足不等式s2-2s≥t2-2t,若1<s<4,则
的取值范围是( )
| 8 |
| cosθ |
| t |
| s |
| A、bc≤16 | ||
B、(-
| ||
C、[-
| ||
D、(-
|
分析:由已知中t满足不等式s2-2s≥t2-2t,根据二次函数y=x2-2x的性质,我们可得s离对应称x=1的距离要远,分别讨论s≥t时与s<t时,
的取值范围即可得到答案.
| t |
| s |
解答:解:s2-2s≥t2-2t,
若s≥t,得s+t≥2,
当s=1时,t≥1,则
≤1
当s=4时,t>-2,
>-
若s<t,得s+t≤2不满足1≤s≤4
故
的取值范围是(-
,1]
故选D
若s≥t,得s+t≥2,
当s=1时,t≥1,则
| t |
| s |
当s=4时,t>-2,
| t |
| s |
| 1 |
| 2 |
若s<t,得s+t≤2不满足1≤s≤4
故
| t |
| s |
| 1 |
| 2 |
故选D
点评:本题考查的知识点是一元二次不等式与一元二次方程,其中根据二次函数与二次不等式之间的关系,将问题转化为二次函数问题,利用二次函数的性质进行解答是解答本题的关键.

练习册系列答案
相关题目
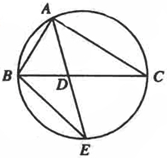 选作题:考生任选一题作答,如果多做,则按所做的第一题计分.
选作题:考生任选一题作答,如果多做,则按所做的第一题计分.