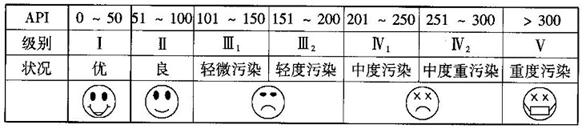
题目内容
将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有1个小球,且每个盒子中的小球个数都不相同,则共有不同的放法( )
| A.15种 | B.18种 | C.19种 | D.21种 |
B
解析试题分析:将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有1个小球,且每个盒子中的小球个数都不相同,那么可能的情况为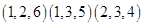 ,当为
,当为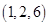 时由不同的盒子知共有
时由不同的盒子知共有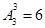 种放法,其余两种也各有6种放法,由分类加法原理知,共有18种放法.
种放法,其余两种也各有6种放法,由分类加法原理知,共有18种放法.
考点:分类加法原理,排列组合.

练习册系列答案
相关题目
5人站成一排,甲、乙两人必须站在一起的不同站法有( )
| A.12种 | B.24种 | C.48种 | D.60种 |
将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有 ( )
| A.12种 | B.10种 | C.9种 | D.8种 |
在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,能被5整除的个数有( )
| A.512 | B.192 | C.240 | D.108 |
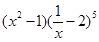 的展开式的常数项是
的展开式的常数项是
| A.48 | B.-48 | C.112 | D.-112 |
一个口袋里装有4个不同的红球,6个不同的白球,若取出一个红球记2分,取出一个白球记1分,从口袋中取出5个球,使总分低于7分的取法共有多少种?()
| A.186 | B.66 | C.60 | D.192 |
S=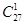 +
+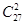 +…+
+…+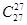 除以9的余数为( )
除以9的余数为( )
| A.8 | B.7 | C.6 | D.5 |
 代表红球,
代表红球,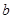 代表蓝球,
代表蓝球,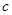 代表黑球,由加法原理及乘法原理,从1个红球和1个篮球中取出若干个球的所有取法可由
代表黑球,由加法原理及乘法原理,从1个红球和1个篮球中取出若干个球的所有取法可由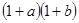 的展开式
的展开式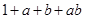 表示出来,如:“1”表示一个球都不取、“
表示出来,如:“1”表示一个球都不取、“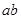 ”用表示把红球和篮球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的篮球都取出或都不取出的所有取法的是
”用表示把红球和篮球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的篮球都取出或都不取出的所有取法的是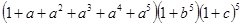
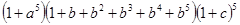
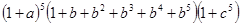
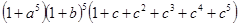
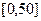 ,
,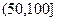 ,
,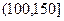 ,
,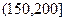 ,
,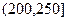 ,
,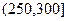 进行分组,得到频率分布直方图如图5.
进行分组,得到频率分布直方图如图5. 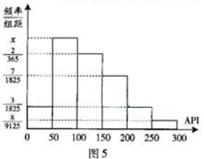
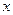 的值;
的值;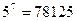 ,
, ,
,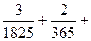
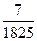
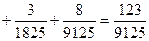 ,
,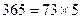 )
)