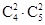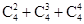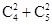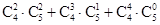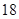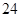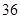题目内容
用 代表红球,
代表红球,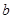 代表蓝球,
代表蓝球,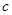 代表黑球,由加法原理及乘法原理,从1个红球和1个篮球中取出若干个球的所有取法可由
代表黑球,由加法原理及乘法原理,从1个红球和1个篮球中取出若干个球的所有取法可由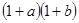 的展开式
的展开式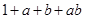 表示出来,如:“1”表示一个球都不取、“
表示出来,如:“1”表示一个球都不取、“ ”表示取出一个红球,面“
”表示取出一个红球,面“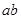 ”用表示把红球和篮球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的篮球都取出或都不取出的所有取法的是
”用表示把红球和篮球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的篮球都取出或都不取出的所有取法的是
A.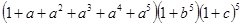 |
B.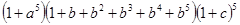 |
C.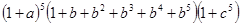 |
D.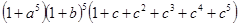 |
A
解析试题分析:依题意所有的篮球都取出或都不取出.所以要有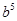 或不含
或不含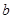 的式子.所以
的式子.所以 符合.故选A.
符合.故选A.
考点:1.新定义.2.二项式展开式.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有1个小球,且每个盒子中的小球个数都不相同,则共有不同的放法( )
| A.15种 | B.18种 | C.19种 | D.21种 |
编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个人的编号与座位号一致的坐法有( )种
| A.10种 | B.20种 | C.60种 | D.90种 |
某城市的街道如图,某人要从A地前往B地,则路程最短的走法有( )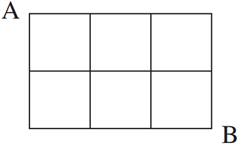
| A.8种 | B.10种 | C.12种 | D.32种 |
在1,2,3,4,5,6这六个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有( )
| A.60个 | B.36个 | C.24个 | D.18个 |
满足a,b∈{-1,0,1,2},且关于x的方程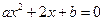 有实数解的有序数对(a,b)的个数为( )
有实数解的有序数对(a,b)的个数为( )
| A.14 |
| B.13 |
| C.12 |
| D.10 |