题目内容
若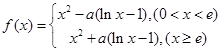 ,其中
,其中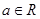 .
.
(1)当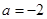 时,求函数
时,求函数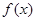 在区间
在区间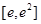 上的最大值;
上的最大值;
(2)当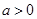 时,若
时,若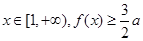 恒成立,求
恒成立,求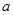 的取值范围.
的取值范围.
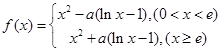 ,其中
,其中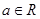 .
.(1)当
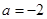 时,求函数
时,求函数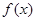 在区间
在区间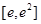 上的最大值;
上的最大值;(2)当
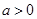 时,若
时,若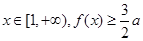 恒成立,求
恒成立,求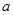 的取值范围.
的取值范围.(1)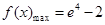 ;(2)
;(2)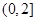 .
.
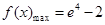 ;(2)
;(2)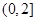 .
.试题分析:本题主要考查导数的运算,利用导数研究函数的单调性,最值和不等式等基础知识,考查函数思想,分类讨论思想,考查综合分析和解决问题的能力.第一问,当
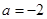 时,函数解析式确定,并不是分段函数,这就降低了试题的难度,求导数,判断所求区间上函数的单调性,再求最值,第一问较简单;第二问,由于函数
时,函数解析式确定,并不是分段函数,这就降低了试题的难度,求导数,判断所求区间上函数的单调性,再求最值,第一问较简单;第二问,由于函数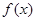 是分段函数,所以根据函数定义域把所求区间从
是分段函数,所以根据函数定义域把所求区间从 断开,充分考查了分类讨论思想,求出每段范围内函数的最小值来解决恒成立问题.
断开,充分考查了分类讨论思想,求出每段范围内函数的最小值来解决恒成立问题.试题解析:(1)当
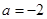 ,
,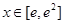 时,
时,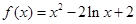 ,
,∵
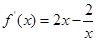 ,∴当
,∴当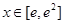 时,
时,  ,
,∴函数
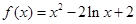 在
在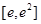 上单调递增,
上单调递增,故
 .(4分)
.(4分)(2)①当
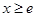 时,
时, ,
, ,
,∵
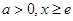 ,∴
,∴ ,∴
,∴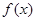 在
在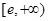 上为增函数,
上为增函数,故当
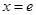 时,
时, ;
;②当
 时,
时, ,
,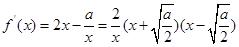 ,
,(ⅰ)当
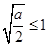 即
即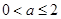 时,
时,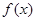 在区间
在区间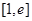 上为增函数,
上为增函数,当
 时,
时,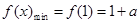 ,且此时
,且此时 ;
;(ⅱ)当
 ,即
,即 时,
时,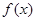 在区间
在区间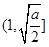 上为减函数,在区间
上为减函数,在区间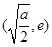 上为增函数,
上为增函数,故当
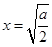 时,
时,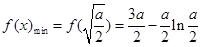 ,且此时
,且此时 ;
;(ⅲ)当
 ,即
,即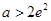 时,
时, 在区间
在区间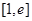 上为减函数,
上为减函数,故当
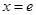 时,
时, .
.综上所述,函数
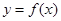 在
在 上的最小值为
上的最小值为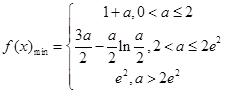
由
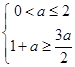 ,得
,得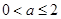 ;由
;由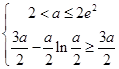 ,得无解;
,得无解;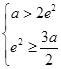 ,得无解;
,得无解;故所求
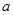 的取值范围是
的取值范围是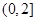 .(12分)
.(12分)
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
 .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值; 的单调区间.
的单调区间.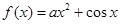 .
.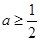 时,函数
时,函数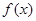 在
在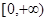 上单调递增;
上单调递增;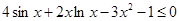 .
.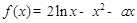 .
.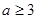 时,讨论函数
时,讨论函数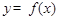 在[
在[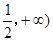 上的单调性;
上的单调性;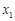 ,
,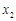
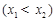 是函数
是函数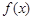 的两个零点,
的两个零点,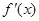 为函数
为函数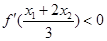 .
.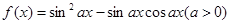 的图象与直线
的图象与直线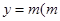 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为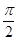
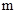 的值;
的值; 是
是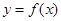 图象的对称中心,且
图象的对称中心,且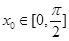 ,求点A的坐标
,求点A的坐标
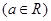 .
.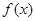 在
在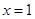 处的切线垂直于直线
处的切线垂直于直线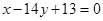 ,求该点的切线方程,并求此时函数
,求该点的切线方程,并求此时函数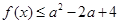 对任意的
对任意的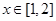 恒成立,求实数
恒成立,求实数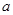 的取值范围.
的取值范围. 的图象在
的图象在 处的切线与圆
处的切线与圆 相切,则
相切,则 的最大值是( )
的最大值是( )

 >f(x),则 ( )
>f(x),则 ( ) f(0)
f(0)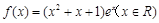 的单调减区间为
的单调减区间为