题目内容
设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=(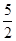 )x,若对任意的x∈[a, a+l],
)x,若对任意的x∈[a, a+l],
不等式f(x+a)≥f2(x)恒成立,则实数a的取值范围是____ 。

解析试题分析: 是定义在
是定义在 上的偶函数,
上的偶函数,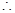 不等式
不等式 恒成立等价为
恒成立等价为 恒成立,
恒成立,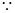 当
当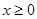 时,
时,
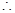 不等式等价为
不等式等价为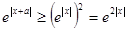 恒成立,
恒成立,
即 在
在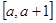 上恒成立,
上恒成立,
平方得 ,
,
即 在
在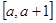 上恒成立,
上恒成立,
设 ,
,
则满足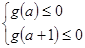
 ,
,
∴ ,
,
即 .
.
考点:1.函数的奇偶性;2.利用函数性质解不等式.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知函数f(x)=-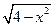 在区间
在区间 上的反函数是其本身,则
上的反函数是其本身,则 可以是 ( )
可以是 ( )
| A.[-2,-1] | B.[-2,0] | C.[0,2] | D. |
 满足
满足 ,则
,则 的取值范围是 .
的取值范围是 .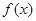 的定义域为
的定义域为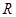 ,
,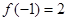 ,对任意
,对任意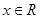 ,
,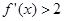 ,则
,则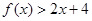 的解
的解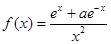 是奇函数,则实数
是奇函数,则实数 的值为 .
的值为 .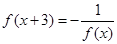 ,且当
,且当 ∈[-3,-2]时,
∈[-3,-2]时,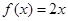 ,则
,则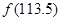 的值是____________.
的值是____________.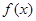 是定义在R上的偶函数,且在区间[0,+∞)上单调递增,则满足不等式
是定义在R上的偶函数,且在区间[0,+∞)上单调递增,则满足不等式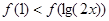 的
的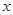 的取值范围是 .
的取值范围是 .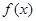 在R上存在导数
在R上存在导数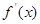 ,对任意的
,对任意的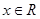 有
有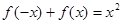 ,且在
,且在 上
上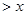 .若
.若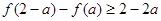 ,则实数
,则实数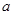 的取值范围 .
的取值范围 .