题目内容
设函数 是定义域在
是定义域在 ,并且满足
,并且满足 ,
, ,且当
,且当 >0时,
>0时, >0。
>0。
(1)求 的值,
的值,
(2)判断函数的奇偶性,
(3)如果 ,求
,求 的取值范围。
的取值范围。
 是定义域在
是定义域在 ,并且满足
,并且满足 ,
, ,且当
,且当 >0时,
>0时, >0。
>0。(1)求
 的值,
的值,(2)判断函数的奇偶性,
(3)如果
 ,求
,求 的取值范围。
的取值范围。(1)0
(2)函数 是R上的奇函数
是R上的奇函数
(3)
(2)函数
 是R上的奇函数
是R上的奇函数(3)

1)令x="y=0" , 则

(2) 令 , 得
, 得 
 故函数
故函数 是R上的奇函数
是R上的奇函数
(3)任取 ,则
,则

 故
故 是R上的增函数
是R上的增函数
∵ ∴
∴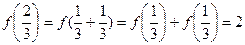
∴ ,又由
,又由 是定义在R上的增函数,得
是定义在R上的增函数,得  解之得
解之得  ,故
,故 


(2) 令
 , 得
, 得 
 故函数
故函数 是R上的奇函数
是R上的奇函数(3)任取
 ,则
,则

 故
故 是R上的增函数
是R上的增函数∵
 ∴
∴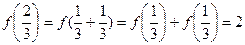
∴
 ,又由
,又由 是定义在R上的增函数,得
是定义在R上的增函数,得  解之得
解之得  ,故
,故 

练习册系列答案
相关题目

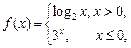 则
则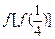 =____▲_____.
=____▲_____.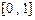 上的函数
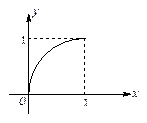
上的函数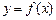 的图像如图所示,对于满足
的图像如图所示,对于满足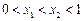 的任意
的任意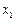 、
、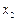 ,给出下列结论:
,给出下列结论: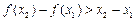 ;
;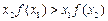 ; ③
; ③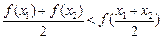 .
.
 是偶函数,且在区间
是偶函数,且在区间 上单调递减,则
上单调递减,则 与
与 的大小关系为( )
的大小关系为( )




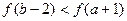
 不能确定
不能确定 , 则
, 则 =_____________.
=_____________. 的定义域为 .
的定义域为 . ,
,
 ,
, 则
则 ( )
( )
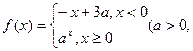 且
且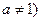 ,在定义域
,在定义域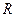 上满足
上满足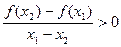 ,则
,则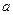 的取值范围是 ( )
的取值范围是 ( )
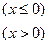 ,使函数值为5的
,使函数值为5的
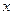 的值是( )
的值是( ) 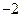
 或
或
