题目内容
下列函数中,周期为1的奇函数是( )
| A.y=sinπ|x| | B.y=|sinπx| | ||
| C.y=-sinπxcosπx | D.y=
|
由函数奇偶性的定义易得y=sinπ|x|,y=|sinπx|为偶函数,故不符合题意.
而y=-sinπxcosπx=-
sin2πx,∴它的周期为
=1,其定义域为R,且f(-x)=-f(x),∴其为奇函数
∵y=
=tan2πx∴它的周期为
=
,也不符合题意
故选C
而y=-sinπxcosπx=-
| 1 |
| 2 |
| 2π |
| 2π |
∵y=
| 2tanπx |
| 1-tan2πx |
| π |
| 2π |
| 1 |
| 2 |
故选C

练习册系列答案
相关题目
下列函数中,周期为1的奇函数是( )
| A、y=1-2sin2πx | ||
B、y=sin (2πx+
| ||
C、y=tg
| ||
| D、y=sinπxcosπx |
下列函数中,周期为1的奇函数是( )
| A、y=sinπ|x| | ||
| B、y=|sinπx| | ||
| C、y=-sinπxcosπx | ||
D、y=
|
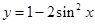 B
B
 D
D