题目内容
下列说法正确的是 .(1)函数
 的图象关于点
的图象关于点 对称;
对称;(2)函数
 的最小正周期是π;
的最小正周期是π;(3)△ABC中,cosA>cosB的充要条件是A<B;
(4)函数y=cos2x+sinx的最小值是-1;
(5)把函数
 的图象向右平移
的图象向右平移 个单位可得到y=2sin2x的图象.
个单位可得到y=2sin2x的图象.
【答案】分析:根据正弦函数的对称性,求出函数 的图象的对称中心坐标,可判断(1)的真假;
的图象的对称中心坐标,可判断(1)的真假;
利用和差角公式,将函数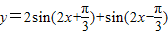 的解析式化为正弦型函数,根据ω值,求出周期,可判断(2)的真假
的解析式化为正弦型函数,根据ω值,求出周期,可判断(2)的真假
根据余弦函数的单调性及三角形内角的范围,可判断(3)的真假
根据三角函数的值域及二次函数的图象和性质,求出函数y=cos2x+sinx的最值可判断(4)的真假
根据在正弦函数平移变换法则,求出平移后的函数解析式,可判断(5)的真假.
解答:解:函数 的图象的对称中心坐标为(
的图象的对称中心坐标为(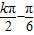 ,0)(k∈Z),故其图象不关于点
,0)(k∈Z),故其图象不关于点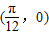 对称,即(1)错误;
对称,即(1)错误;
函数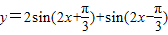 =
=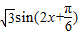 ,其周期是π,故(2)正确
,其周期是π,故(2)正确
y=cosx在(0,π)上单调递减,故△ABC中,cosA>cosB的充要条件是A<B,即(3)正确;
函数y=cos2x+sinx=1-sin2x+sinx,当sinx=-1时,函数取最小值-1,故(4)正确;
把函数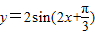 的图象向右平移
的图象向右平移 个单位可得
个单位可得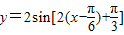 =2sin2x的图象,故(5)正确.
=2sin2x的图象,故(5)正确.
故答案为:(2)(3)(4)(5)
点评:本题以命题的真假判断为载体考查了三角函数的对称性,周期性,单调性,最值,及平移变换,是三角函数的综合应用.
 的图象的对称中心坐标,可判断(1)的真假;
的图象的对称中心坐标,可判断(1)的真假;利用和差角公式,将函数
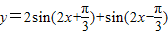 的解析式化为正弦型函数,根据ω值,求出周期,可判断(2)的真假
的解析式化为正弦型函数,根据ω值,求出周期,可判断(2)的真假根据余弦函数的单调性及三角形内角的范围,可判断(3)的真假
根据三角函数的值域及二次函数的图象和性质,求出函数y=cos2x+sinx的最值可判断(4)的真假
根据在正弦函数平移变换法则,求出平移后的函数解析式,可判断(5)的真假.
解答:解:函数
 的图象的对称中心坐标为(
的图象的对称中心坐标为(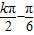 ,0)(k∈Z),故其图象不关于点
,0)(k∈Z),故其图象不关于点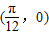 对称,即(1)错误;
对称,即(1)错误;函数
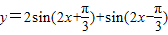 =
=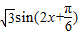 ,其周期是π,故(2)正确
,其周期是π,故(2)正确y=cosx在(0,π)上单调递减,故△ABC中,cosA>cosB的充要条件是A<B,即(3)正确;
函数y=cos2x+sinx=1-sin2x+sinx,当sinx=-1时,函数取最小值-1,故(4)正确;
把函数
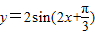 的图象向右平移
的图象向右平移 个单位可得
个单位可得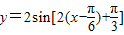 =2sin2x的图象,故(5)正确.
=2sin2x的图象,故(5)正确.故答案为:(2)(3)(4)(5)
点评:本题以命题的真假判断为载体考查了三角函数的对称性,周期性,单调性,最值,及平移变换,是三角函数的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目