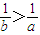题目内容
若b<0<a(a,b∈R),则下列不等式中正确的是
- A.b2<a2
- B.
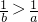
- C.-b<-a
- D.a-b>a+b
D
分析:取b=-2,a=1代入可排除A,B,再取b=-1,a=2代入可排除C,而选项D可由不等式的性质证明.
解答:∵b<0<a,不妨取b=-2,a=1,可得a2=1,b2=4,显然满足a2<b2,故可排除A;
仍取b=-2,a=1,可得 =
= ,
, =1,显然满足
=1,显然满足 ,故可排除B;
,故可排除B;
取b=-1,a=2,可得-b=1,-a=-2,显然-b>-a,故可排除C;
由b<0<a可得-b>b,两边同时加上a可得a-b>a+b,故正确,
故选D
点评:本题考查不等关系的判断,反例法是解决问题的关键,属基础题.
分析:取b=-2,a=1代入可排除A,B,再取b=-1,a=2代入可排除C,而选项D可由不等式的性质证明.
解答:∵b<0<a,不妨取b=-2,a=1,可得a2=1,b2=4,显然满足a2<b2,故可排除A;
仍取b=-2,a=1,可得
 =
= ,
, =1,显然满足
=1,显然满足 ,故可排除B;
,故可排除B;取b=-1,a=2,可得-b=1,-a=-2,显然-b>-a,故可排除C;
由b<0<a可得-b>b,两边同时加上a可得a-b>a+b,故正确,
故选D
点评:本题考查不等关系的判断,反例法是解决问题的关键,属基础题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目