题目内容
在三棱锥S-ABC中，∠SAB=∠SAC=∠ACB=90°，AC=2，BC=| 13 |
| 29 |
（1）求证：SC⊥BC；
（2）求SC与AB所成角的余弦值．
分析：解法一：建系，写出有关点的坐标，B，C，s，（1）要证SC⊥BC；只要证EF⊥面PAB，只要证）
•
=0即可；
（2）要求异面直线SC与AB所成的角的余弦值，只要求
与
所成角的余弦值即可；
解法二：综合法证明，（1）要证SC⊥BC，只要证AC⊥BC即可；
（2）要求SC与AB所成角的余弦值，通过平移找到SC与AB所成角，解三角形即可．
| SC |
| CB |
（2）要求异面直线SC与AB所成的角的余弦值，只要求
| SC |
| AB |
解法二：综合法证明，（1）要证SC⊥BC，只要证AC⊥BC即可；
（2）要求SC与AB所成角的余弦值，通过平移找到SC与AB所成角，解三角形即可．
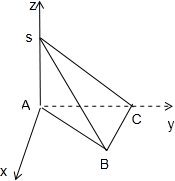
解答：解法一：如图，取A为原点，AB、AS分别为y、z轴建立空间直角坐标系，
∵AC=2，BC=
，SB=
，∴B（0，
，0）、S（0，0，2
）、C（2
，
，0），
=（2
，
，-2
），
=（-2
，
，0）．
（1）∵
•
=0，∴SC⊥BC．
（2）设SC与AB所成的角为α，
∵
=（0，
，0），
•
=4，|
||
|=4
，
∴cosα=
，即为所求．
解法二：（1）∵SA⊥面ABC，AC⊥BC，AC是斜线SC在平面ABC内的射影，∴SC⊥BC．
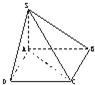（2）如图，过点C作CD∥AB，过点A作AD∥BC交CD于点D，
连接SD、SC，则∠SCD为异面直线SC与AB所成的角．
∵四边形ABCD是平行四边形，CD=
，SA=2
，SD=
=
=5，
∴在△SDC中，由余弦定理得cos∠SCD=
，即为所求．
∵AC=2，BC=
| 13 |
| 29 |
| 17 |
| 3 |
|
| 4 | ||
|
| SC |
|
| 4 | ||
|
| 3 |
| CB |
|
| 13 | ||
|
（1）∵
| SC |
| CB |
（2）设SC与AB所成的角为α，
∵
| AB |
| 17 |
| SC |
| AB |
| SC |
| AB |
| 17 |
∴cosα=
| ||
| 17 |
解法二：（1）∵SA⊥面ABC，AC⊥BC，AC是斜线SC在平面ABC内的射影，∴SC⊥BC．
（2）如图，过点C作CD∥AB，过点A作AD∥BC交CD于点D，连接SD、SC，则∠SCD为异面直线SC与AB所成的角．
∵四边形ABCD是平行四边形，CD=
| 17 |
| 3 |
| SA2+AD2 |
| 12+13 |
∴在△SDC中，由余弦定理得cos∠SCD=
| ||
| 17 |
点评：考查利用空间向量证明垂直和求夹角和距离问题，以及面面垂直的判定定理，体现 了转化的思想方法，l利用综合法求异面直线所成的角，关键是找出这个角，把空间角转化为平面角求解，体现了转化的思想，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为边长为1的等边三角形，∠BAC=90°，O为BC中点．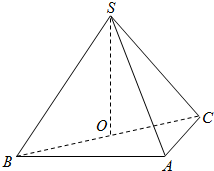
如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC=90°，O为BC中点．
如图，在三棱锥S-ABC中，侧面SAB⊥底面ABC，且∠ASB=∠ABC=90°，AS=SB=2，
C．
如图，在三棱锥S-ABC中，