题目内容
若a,b∈R+,且a+b=1,则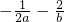 的最大值是________.
的最大值是________.
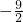
分析:将
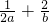 转化成(
转化成(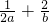 )(a+b),然后化简整理利用基本不等式可求出
)(a+b),然后化简整理利用基本不等式可求出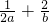 的最值,从而求出所求.
的最值,从而求出所求.解答:∵a,b∈R+,且a+b=1
∴
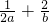 =(
=(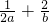 )(a+b)=
)(a+b)= +2+
+2+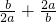 ≥
≥ +2
+2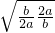 =
=
当且仅当a=
 ,b=
,b= 时取等号
时取等号∴
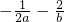 ≤
≤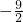
即
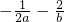 的最大值是
的最大值是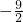
故答案为:
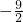
点评:本题主要考查基本不等式,着重考查整体代换的思想,易错点在于应用基本不等式时需注意“一正二定三等”三个条件缺一不可,属于基础题.

练习册系列答案
相关题目