题目内容
(14分)直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B.
(1)求实数k的取值范围;
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
【答案】
(1)-2<k<- .(2) k=-
.(2) k=- .
.
【解析】(1)直线与双曲线方程联立消y得关于x的一元二次方程,根据判别式大于零,可求出k的取值范围.
(2) 解本题的突破口是假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0),则由FA⊥FB得(x1-c)(x2-c)+y1y2=0,即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0,
整理得:(k2+1)x1x2+(k-c)(x1+x2)+c2+1=0再根据韦达定理解决即可.
(1)将直线l的方程y=kx+1代入双曲线方程2x2-y2=1后,整理得:
(k2-2)x2+2kx+2=0①
解:依题意,直线l与双曲线C的右支交于不同两点,故
 ,解得-2<k<-
,解得-2<k<- .
.
(2)设A、B两点的坐标分别为(x1,y1),(x2,y2),则由①式得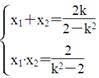 ②,
②,
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0),则由FA⊥FB得(x1-c)(x2-c)+y1y2=0,即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0,
整理得:(k2+1)x1x2+(k-c)(x1+x2)+c2+1=0③
把②式及c=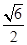 代入③式化简得5k2+2
代入③式化简得5k2+2 k-6=0,解得
k-6=0,解得
k=- 或k=
或k=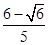 ∉(-2,-
∉(-2,- )(舍去).
)(舍去).
可得k=- 使得以线段AB为直径的圆经过双曲线C的右焦点.
使得以线段AB为直径的圆经过双曲线C的右焦点.

练习册系列答案
相关题目
某大型企业2010年和2011年进行科技创新,企业有效转型,产品大规模升级,该企业2012年季度利润和季度能源成本分别为x、y,其值见表,x单位为千万元,y单位为十万元.下面四个结论:
①点(x,y)构成的图形是散点图,这些点不在一条直线上;
②季度利润与季度能源成本正相关;
③若直线l:
=
x+
是季度能源成本与季度利润的回归直线,则直线l经过点(32,15);
④由表可知2013年春季的利润为3.55亿元,能源成本为100万元.
其中正确的是 (只填结论番号,多填少填错填均得零分).
| 季度 | 1 | 2 | 3 | 4 |
| x | 30 | 31 | 33 | 34 |
| y | 18 | 16 | 14 | 12 |
②季度利润与季度能源成本正相关;
③若直线l:
| ? |
| y |
| ? |
| b |
| ? |
| a |
④由表可知2013年春季的利润为3.55亿元,能源成本为100万元.
其中正确的是