题目内容
(08年周至二中四模理)( 14分)
直线l:ax-y-1=0与曲线C:x2-2y2=1交于P、Q两点,
(1)当实数a为何值时,|PQ|=2![]() .
.
(2)是否存在a的值,使得以PQ为直径的圆经过原点?若存在,求出a的值;若不存在,说明理由.
解析:(1)设P(x1,y1),Q(x2,y2),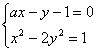 , ∴(1-2a2)x2+4ax-3=0.
, ∴(1-2a2)x2+4ax-3=0.
若1-2a2=0,即a=±![]() 时,l与C的渐近线平行,l与C只有一个交点,与题意不合,
时,l与C的渐近线平行,l与C只有一个交点,与题意不合,
∴1-2a2≠0,Δ=(4a)2-4(1-2a2)(-3)>0, ∴-![]() <a<
<a<![]() .
.
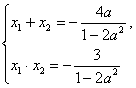 (*) ∴|PQ|=
(*) ∴|PQ|=![]() |x1-x2|=2
|x1-x2|=2![]() .
.
∴(x1-x2)2=4,∴(x1+x2)2-4x1x2=4. ∴(-![]() )2-4
)2-4![]() =4.
=4.
∴a=±1∈(-![]() ,
,![]() ).
).
∴所求的实数a的值为a=±1. 6分
(2)假设存在实数a,使得以PQ为直径的圆经过原点O,则由OP⊥OQ,得y1?y2=-x1?x2.
∴(ax1-1)?(ax2-1)=-x1?x2,
∴(1+a2)x1?x2-a(x1+x2)+1=0. 10分
把(*)式代入得:a2=-2与a为实数矛盾,
∴不存在实数a使得以PQ为直径的圆经过原点. 10分

练习册系列答案
相关题目