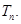题目内容
数列 满足
满足 .
.
(1)计算 ,
, ,
, ,
,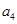 ,由此猜想通项公式
,由此猜想通项公式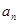 ,并用数学归纳法证明此猜想;
,并用数学归纳法证明此猜想;
(2)若数列 满足
满足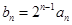 ,求证:
,求证: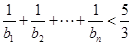 .
.
(1)1,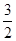 ,
,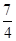 ,
,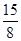 an=
an=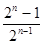 (n∈N*).
(n∈N*).
(2)运用数学归纳法证明来分为两步骤来加以证明即可。
【解析】
试题分析:解:(1)当n=1时,a1=S1=2-a1,∴a1=1.
当n=2时,a1+a2=S2=2×2-a2,∴a2=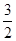 . 1分
. 1分
当n=3时,a1+a2+a3=S3=2×3-a3,∴a3=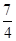 .
.
当n=4时,a1+a2+a3+a4=S4=2×4-a4,∴a4=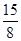 . 2分
. 2分
由此猜想an=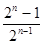 (n∈N*). 4分
(n∈N*). 4分
现用数学归纳法证明如下:
①当n=1时, a1=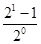 =1,结论成立.
=1,结论成立.
②假设n=k(k≥1且k∈N*)时,结论成立,即ak=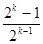 ,那么当n=k+1时,
,那么当n=k+1时,
ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak=2+ak-ak+1,
∴2ak+1=2+ak,∴ak+1=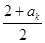 =
=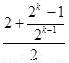 =
=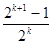 ,故当n=k+1时,结论成立,
,故当n=k+1时,结论成立,
由①②知猜想an=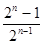 (n∈N*)成立. 8分
(n∈N*)成立. 8分
(2)由(1)知,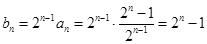 ,
,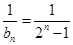 . 9分
. 9分
解法1:当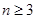 时,
时,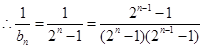
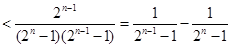 10分
10分
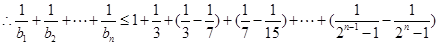
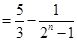
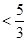 . 12分
. 12分
解法2:当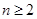 时,
时,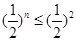 ,
,
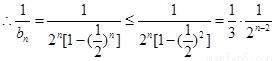 10分
10分
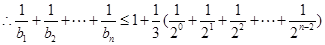
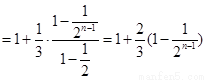
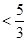 . 12分
. 12分
解法3:
当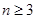 时,
时,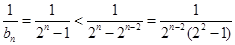 10分
10分
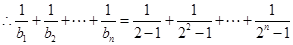
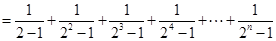
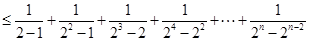

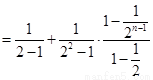
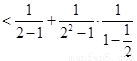
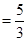 . 12分
. 12分
考点:数学归纳法证明
点评:主要是考查了数列的猜想以及数学归纳法的运用,属于基础题。

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案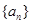 满足:
满足: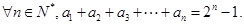
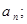
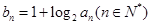 ,
,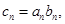 求数列
求数列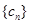 的前n项和
的前n项和