题目内容
已知整数数列![]() 满足:
满足:![]() ,
,![]() .
.
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 将数列![]() 中的所有项依次按如图所示的规律循环地排成如下三角形数表:
中的所有项依次按如图所示的规律循环地排成如下三角形数表:

……
依次计算各个三角形数表内各行中的各数之和,设由这些和按原来行的前后顺序构成的数列为![]() ,
,
求![]() 的值;
的值;
(3) 令![]() (
(![]() 为大于等于
为大于等于![]() 的正整数),问数列
的正整数),问数列![]() 中是否存在连续三项成等比数列?
中是否存在连续三项成等比数列?
若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
解:(1)因为数列![]() 是整数列,所以
是整数列,所以![]() 是整数, 所以
是整数, 所以![]() 都是整数,
都是整数,
又![]() ,所以
,所以![]() .……3分
.……3分
即数列![]() 是首项为1,公差
是首项为1,公差![]() 的等差数列,
的等差数列,
所以![]() . ……………5分
. ……………5分
(2)设每一个循环(4行)记为一组,由于每一个循环含有4行,
故![]() 是第25个循环中第4行中各数之和. ……………6分
是第25个循环中第4行中各数之和. ……………6分
由循环分组规律知,每个循环共有10项,
故第25个循环中的第4行内的4个数分别为数列![]() 的第247项至第250项,又
的第247项至第250项,又![]() ,
,
所以![]() .…8分
.…8分
又![]() ,所以
,所以![]() . ……………10分
. ……………10分
(3)因为![]() , 设数列
, 设数列![]() 中,
中,![]() 成等比数列,
成等比数列,
即![]() ,所以
,所以![]() .
.
化简得![]() . (*) ……………12分
. (*) ……………12分
当![]() 时,
时,![]() ,等式(*)成立,而
,等式(*)成立,而![]() ,故等式(*)不成立;
,故等式(*)不成立;
当![]() 时,
时,![]() ,等式(*)成立;
,等式(*)成立;
当![]() 时,
时,![]() ,这与
,这与![]() 矛盾,
矛盾,
这时等式(*)不成立. ………… …14分
综上所述,当![]() 时,数列
时,数列![]() 中不存在连续三项成等比数列;
中不存在连续三项成等比数列;
当![]() 时,数列
时,数列![]() 中的第二、三、四项成等比数列,这三项依次是18,30,50. ………16分
中的第二、三、四项成等比数列,这三项依次是18,30,50. ………16分

练习册系列答案
相关题目

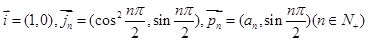 ,数列
,数列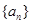 满足:
满足: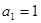 ,
,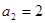 ,
,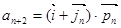 .
.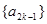 是等差数列;数列
是等差数列;数列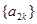 是等比数列;(其中
是等比数列;(其中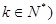 ;
;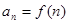 ,对任意的正整数
,对任意的正整数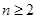 ,不等式
,不等式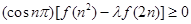 恒成立,求
恒成立,求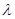 的取值范围.
的取值范围. 中,如果存在非零常数
中,如果存在非零常数 ,使得
,使得 对于任意非零正整数
对于任意非零正整数 均成立,那么就称数列
均成立,那么就称数列 满足
满足 (
( )且
)且 ,
,
 ,当
,当