题目内容
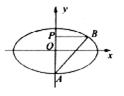
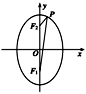
如图所示,点P是椭圆![]() =1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
=1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
8-4![]()
解析:
在椭圆![]() =1中,
=1中,
a=![]() ,b=2.∴c=
,b=2.∴c=![]() =1.
=1.
又∵点P在椭圆上,
∴|PF1|+|PF2|=2a=2![]() . ①
. ①
由余弦定理知:
|PF1|2+|PF2|2-2|PF1||PF2|cos30°
=|F1F2|2=(2c)2=4. ②
①式两边平方得
|PF1|2+|PF2|2+2|PF1|·|PF2|=20, ③
③-②得(2+![]() )|PF1|·|PF2|=16,
)|PF1|·|PF2|=16,
∴|PF1|·|PF2|=16(2-![]() ), ∴
), ∴![]() =
=![]() |PF1|·|PF2|sin30°=8-4
|PF1|·|PF2|sin30°=8-4![]() .
.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
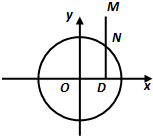 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且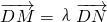 (λ>0).
(λ>0).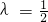 时,(1)所得曲线记为C,已知直线
时,(1)所得曲线记为C,已知直线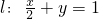 ,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.
,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.