题目内容
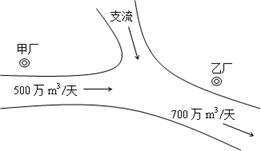
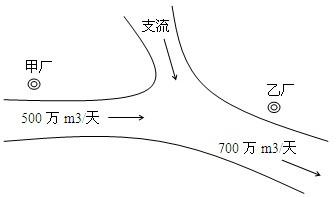
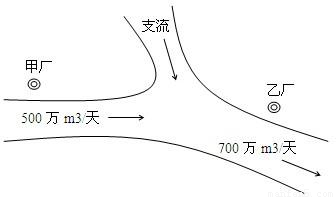
如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.(Ⅰ)设甲、乙两个化工厂每天各自处理的污水分别为x、y万m3,试根据环保部门的要求写出x、y所满足的所有条件;
(Ⅱ)已知甲厂处理污水的成本是1200元/万m3,乙厂处理污水的成本是1000元/万m3,在满足环保部门要求的条件下,甲、乙两个化工厂每天应分别各自处理污水多少万m3,才能使这两个工厂处理污水的总费用最小?最小总费用是多少元?
【答案】分析:利用线性规划的思想方法解决某些实际问题属于直线方程的一个应用.本题主要考查找出约束条件与目标函数,准确地描画可行域,再利用图形直线求得满足题设的最优解.(1)要写出x、y所满足的所有条件,我们需要考虑如下几个方面①处理量不能超过自己的排放量②甲厂的污水在自然净化后不能超过0.2%③甲、乙两厂的污水排放量在河水中比例不能超过0.2%.(2)由甲厂处理污水的成本是1200元/万m3,乙厂处理污水的成本是1000元/万m3,我们可以列出目标函数,然后画出满足(1)中约束条件的可行域,然后利用平移直线法,易求出最优解.
解答: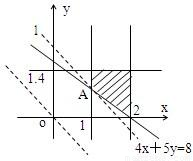 解:(Ⅰ)据题意,x、y所满足的所有条件是
解:(Ⅰ)据题意,x、y所满足的所有条件是
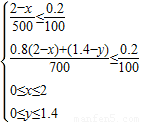 ,即
,即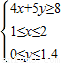
(Ⅱ)设甲、乙两厂处理污水的总费用为z元,
则目标函数z=1200x+1000y=200(6x+5y).
作可行域,如图平移直线l:6x+5y=0,当直线经过点A(1,0.8)时,
z取最大值,此时z=1200×1+1000×0.8=2000(元).
故甲、乙两厂每天应分别处理1万m3、0.8万m3污水,
才能使两厂处理污水的总费用最小,且最小总费用是2000元.
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.
解答:
 解:(Ⅰ)据题意,x、y所满足的所有条件是
解:(Ⅰ)据题意,x、y所满足的所有条件是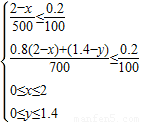 ,即
,即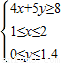
(Ⅱ)设甲、乙两厂处理污水的总费用为z元,
则目标函数z=1200x+1000y=200(6x+5y).
作可行域,如图平移直线l:6x+5y=0,当直线经过点A(1,0.8)时,
z取最大值,此时z=1200×1+1000×0.8=2000(元).
故甲、乙两厂每天应分别处理1万m3、0.8万m3污水,
才能使两厂处理污水的总费用最小,且最小总费用是2000元.
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
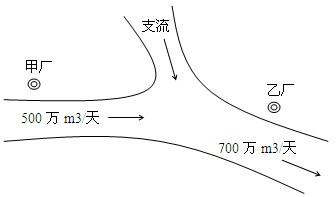 如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.
如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.