题目内容
(满分12分)在锐角△ABC中,已知内角A、B、C所对的边分别为a、b、c,且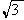 (tanA-tanB)=1+tanA·tanB.
(tanA-tanB)=1+tanA·tanB.
(1)若a2-ab=c2-b2,求A、B、C的大小;
(2)已知向量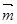 =(sinA,cosA),
=(sinA,cosA),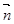 =(cosB,sinB),求|3
=(cosB,sinB),求|3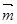 -2
-2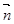 |的取值范围.
|的取值范围.
(1)A=5π /12 ,B=π /4 . C=π/ 3;(2)1≤|3m-2n|< 7 .
【解析】本试题主要是考查了解三角形中余弦定理的运用,以及两角差的正切公式的运用,以及向量的数量积综合运用问题,三角函数的性质等等知识点的交汇处命题。
(1)先将已知的正切关系式化简,再利用余弦定理得到角A,B,C的值
(2)因为向量的模的平方就是向量的平方,那么可知,结合角的范围可知得到三角函数的值域。
解:因为 3 (tanA-tanB)=1+tanA•tanB,
所以tan(A-B)=(tanA-tanB) /(1+tanA•tanB) = 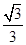 ,
,
∴A-B=π/ 6 .…(2分)
(1)因为a2+b2-2abcosC=c2,所以cosC=1/ 2 ,∴C=π/ 3 ,…(4分)
A+B=2π/ 3 ,又A-B=π/ 6 ,
∴A=5π /12 ,B=π /4 .…(6分)
(2)因为向量 m =(sinA,cosA), n =(cosB,sinB),
∴|3 m -2 n |2=13-12 m • n =13-12sin(A+B)=13-12sin(2A-π 6 )…(8分) 0<A<π 2 0<B<π/ 2 0<C<π/ 2 ⇒ 0<A<π /2 0<A-π /6 <π /2 0<π-2A+π/ 6 <π/ 2 ⇒π/ 6 <A<π/ 2 .…(10分)
π /6 <2A-π /6 <5π/ 6 ,6<12sina(2A-π /6 )≤12,
1≤|3m-2n|< 7 .…(12分)

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案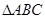 中,
中,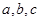 分别为角
分别为角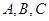 的对边,且
的对边,且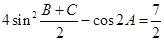 .
.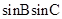 的最大值.
的最大值. 中,
中, 分别是内角
分别是内角 所对的边,且
所对的边,且 .
. 的大小;
的大小; ,且
,且 ,求
,求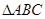 中,角
中,角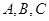 所对边分别为
所对边分别为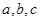 ,已知
,已知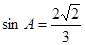 .
.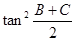 的值;
的值;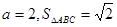 ,求
,求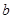 的值.
的值. 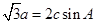 。
。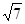 ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值。
,求a+b的值。