题目内容
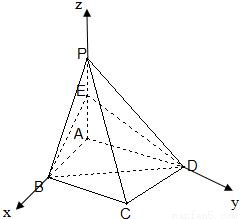
 如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),
如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),(I)在棱PA上是否存在点E,使得PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论;若不存在,说明理由;
(II)求二面角B-PC-D的大小.(若不是特殊角请用反三角函数表示)
【答案】分析:(I)以A为原点,AB,AD,AP分别为x轴,y轴,z轴建立坐标系A-xyz.设E(0,0,a),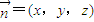 为平面EBD的法向量,
为平面EBD的法向量,
利用 求出
求出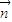 ,利用
,利用 求出a,在棱PA上存在点E,使得PC∥平面EBD.求出PE:PA的值.
求出a,在棱PA上存在点E,使得PC∥平面EBD.求出PE:PA的值.
(II)设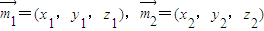 分别为平面BPC和平面DPC的法向量,求出法向量,
分别为平面BPC和平面DPC的法向量,求出法向量,
利用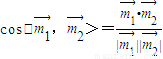 求二面角B-PC-D的大小.(若不是特殊角请用反三角函数表示)
求二面角B-PC-D的大小.(若不是特殊角请用反三角函数表示)
解答:解:由三视图可知,多面体是四棱锥P-ABCD,底面ABCD是直角梯形,侧棱PA⊥平面ABCD.且PA=2,AB=BC=1,AD=2.(1分)
如图以A为原点,AB,AD,AP分别为x轴,y轴,z轴建立坐标系A-xyz.
由三视图可知,B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).(3分)
设E(0,0,a), 为平面EBD的法向量,
为平面EBD的法向量,
则 ,
, ,
,
由 ,得
,得 .
.
令y=1,则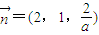 .(4分)
.(4分)
又 ,且
,且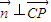 ,
,
∴ ,
,
∴a= ..(5分)
..(5分)
∴在棱PA上存在点E,使得PC∥平面EBD,
此时PE:PA=1:3..(6分)
(Ⅱ)设 分别为平面BPC和平面DPC的法向量,
分别为平面BPC和平面DPC的法向量,
又 ,
,
则由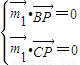 ,得
,得 ,
,
令z1=1,则 .(9分)
.(9分)
同理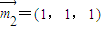 .
.
∴ .(11分)
.(11分)
由图可知二面角B-PC-D为钝二面角,
∴二面角B-PC-D的大小为 .(12分)
.(12分)
点评:本题考查直线与平面平行的判定,二面角及其度量,考查转化思想,计算能力,是中档题.
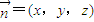 为平面EBD的法向量,
为平面EBD的法向量,利用
 求出
求出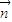 ,利用
,利用 求出a,在棱PA上存在点E,使得PC∥平面EBD.求出PE:PA的值.
求出a,在棱PA上存在点E,使得PC∥平面EBD.求出PE:PA的值.(II)设
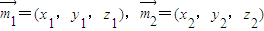 分别为平面BPC和平面DPC的法向量,求出法向量,
分别为平面BPC和平面DPC的法向量,求出法向量,利用
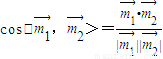 求二面角B-PC-D的大小.(若不是特殊角请用反三角函数表示)
求二面角B-PC-D的大小.(若不是特殊角请用反三角函数表示)解答:解:由三视图可知,多面体是四棱锥P-ABCD,底面ABCD是直角梯形,侧棱PA⊥平面ABCD.且PA=2,AB=BC=1,AD=2.(1分)
如图以A为原点,AB,AD,AP分别为x轴,y轴,z轴建立坐标系A-xyz.
由三视图可知,B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).(3分)
设E(0,0,a),
 为平面EBD的法向量,
为平面EBD的法向量,则
 ,
, ,
,由
 ,得
,得 .
.
令y=1,则
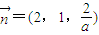 .(4分)
.(4分)又
 ,且
,且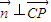 ,
,∴
 ,
,∴a=
 ..(5分)
..(5分)∴在棱PA上存在点E,使得PC∥平面EBD,
此时PE:PA=1:3..(6分)
(Ⅱ)设
 分别为平面BPC和平面DPC的法向量,
分别为平面BPC和平面DPC的法向量,又
 ,
,则由
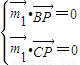 ,得
,得 ,
,令z1=1,则
 .(9分)
.(9分)同理
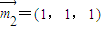 .
.∴
 .(11分)
.(11分)由图可知二面角B-PC-D为钝二面角,
∴二面角B-PC-D的大小为
 .(12分)
.(12分)点评:本题考查直线与平面平行的判定,二面角及其度量,考查转化思想,计算能力,是中档题.

练习册系列答案
相关题目
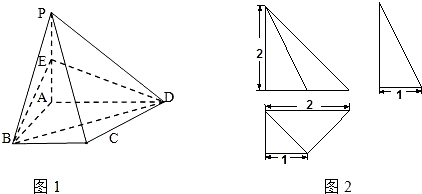
 如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),
如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2), 如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),
如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2), 如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),
如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),