题目内容
在锐角三角形ABC中，A=2B，
、
、
所对的角分别为A、B、C，则
的范围是 。
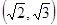
解析试题分析：锐角△ABC中，角A、B、C所对的边分别为a、b、c，A=2B，∴0＜2B＜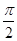
,
且 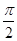＜3B＜π．∴
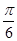＜B＜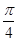
，∴
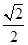＜cosB＜
． 由正弦定理可得 =
。
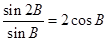
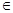
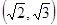考点：三角形内角和定理，正弦定理的应用，二倍角的正弦，三角函数的性质。
点评：中档题，本题较为典型，综合性也较强。解题的关键是注意确定角B的范围。
练习册系列答案
相关题目
的三个内角
满足
，则角
的取值范围是 ．
、b、c ，若
，则
。
，当竹竿滑动到A1B1位置时，
，竹竿在滑动时中点T也沿着某种轨迹运动到T1点，则T运动的路程是_________米.
中，角A，B，C所对的边分别是
，且
,
. 
，则
= 
是半圆
的直径，点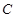
在半圆上，
，垂足为
，且
，设
，则
的值为 _________；
中，角
和
满足
，那么
中，已知点
在
边上，
,
, 
,则
的长为_____ 