题目内容
设平面向量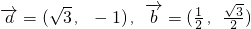 ,若存在实数m(m≠0)和角θ,其中
,若存在实数m(m≠0)和角θ,其中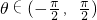 ,使向量
,使向量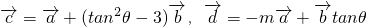 ,且
,且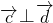 .
.
(1)求m=f(θ)的关系式;
(2)若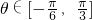 ,求f(θ)的最小值,并求出此时的θ值.
,求f(θ)的最小值,并求出此时的θ值.
解:(1)∵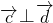 ,
,
且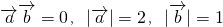 ,
,
∴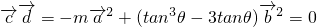
∴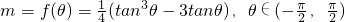
(2)设t=tanθ,
又∵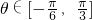 ,
,
∴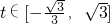 ,
,
则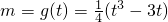
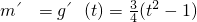 ,
,
令g'(t)=0得t=-1(舍去) t=1
∴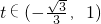 时,
时,
g'(t)<0,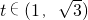 时,
时,
g'(t)>0,
∴t=1时,即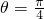 时,
时,
g(1)为极小值也是最小值,g(t)最小值为 .
.
分析:(1)由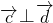 ,且
,且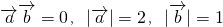 ,知
,知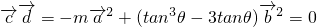 ,由此能求出m=f(θ)的关系式.
,由此能求出m=f(θ)的关系式.
(2)设t=tanθ,由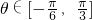 ,知
,知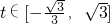 ,则
,则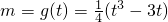
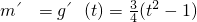 ,由此能求出f(θ)的最小值,并能求出此时的θ值.
,由此能求出f(θ)的最小值,并能求出此时的θ值.
点评:本题考查平面向量的综合运用,解题时要认真审题,仔细解答,注意三角函数恒等变换的灵活运用.
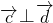 ,
,且
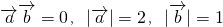 ,
,∴
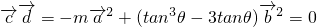
∴
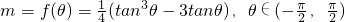
(2)设t=tanθ,
又∵
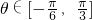 ,
,∴
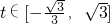 ,
,则
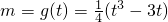
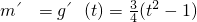 ,
,令g'(t)=0得t=-1(舍去) t=1
∴
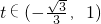 时,
时,g'(t)<0,
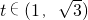 时,
时,g'(t)>0,
∴t=1时,即
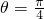 时,
时,g(1)为极小值也是最小值,g(t)最小值为
 .
.分析:(1)由
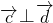 ,且
,且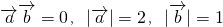 ,知
,知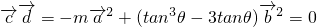 ,由此能求出m=f(θ)的关系式.
,由此能求出m=f(θ)的关系式.(2)设t=tanθ,由
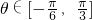 ,知
,知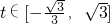 ,则
,则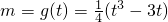
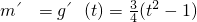 ,由此能求出f(θ)的最小值,并能求出此时的θ值.
,由此能求出f(θ)的最小值,并能求出此时的θ值.点评:本题考查平面向量的综合运用,解题时要认真审题,仔细解答,注意三角函数恒等变换的灵活运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 使得
使得 ,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。 ,则a、b线性相关;
,则a、b线性相关; 使得
使得 ,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。 ,则a、b线性相关;
,则a、b线性相关;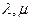 使得
使得 ,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。
,则除a、b线性相关,下面的命题中,a、b、c均为已知平面M上的向量。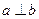 ,则a、b线性相关;
,则a、b线性相关;