题目内容
函数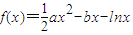 ,a>0,f'(1)=0.
,a>0,f'(1)=0.(1)①试用含有a的式子表示b;②求f(x)的单调区间;
(2)对于函数图象上的不同两点A(x1,y1),B(x2,y2),如果在函数图象上存在点P(x,y)(其中x在x1与x2之间),使得点P处的切线l∥AB,则称AB存在“伴随切线”,当
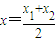 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图象上是否存在两点A、B,使得AB存在“中值伴随切线”?若存在,求出A、B的坐标;若不存在,说明理由.
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图象上是否存在两点A、B,使得AB存在“中值伴随切线”?若存在,求出A、B的坐标;若不存在,说明理由.
【答案】分析:(1)①先求导函数,再利用f'(1)=0,可用含有a的式子表示b;②求导函数,再利用导数大于0的函数的单调增区间,导数小于0得函数的单调减区间;
(2)对于存在性问题,可先假设存在,即假设存在两点A(x1,y1),B(x2,y2),再利用中值伴侣切线的意义结合导数工具,求出g(t)在(1,+∞)上单调递增,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)①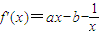
∵f'(1)=0,∴b=a-1.(2分)
②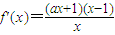
∵x>0,a>0
∴当x>1时f'(x)>0,当0<x<1时,f'(x)<0
∴f(x)增区间为(1,+∞),减区间为(0,1)(6分)
(2)不存在 (7分) (反证法)
若存在两点A(x1,y1),B(x2,y2),不妨设0<x1<x2,
则曲线y=f(x)在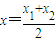 的切线斜率
的切线斜率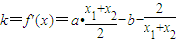
又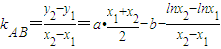
∴由k=kAB得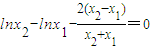 ①(11分)
①(11分)
令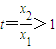 ,则①化为
,则①化为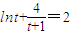 ②
②
令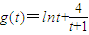 (t>1)
(t>1)
∵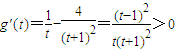
∴g(t)在(1,+∞)为增函数 (15分)
又t>1∴g(t)>g(1)=2此与②矛盾,
∴不存在 (16分)
点评:本题以函数为载体,考查导数的运用,考查函数的单调性,考查存在性问题,关键是对新定义的理解.
(2)对于存在性问题,可先假设存在,即假设存在两点A(x1,y1),B(x2,y2),再利用中值伴侣切线的意义结合导数工具,求出g(t)在(1,+∞)上单调递增,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)①
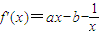
∵f'(1)=0,∴b=a-1.(2分)
②
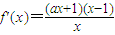
∵x>0,a>0
∴当x>1时f'(x)>0,当0<x<1时,f'(x)<0
∴f(x)增区间为(1,+∞),减区间为(0,1)(6分)
(2)不存在 (7分) (反证法)
若存在两点A(x1,y1),B(x2,y2),不妨设0<x1<x2,
则曲线y=f(x)在
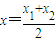 的切线斜率
的切线斜率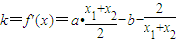
又
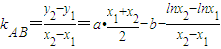
∴由k=kAB得
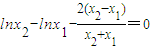 ①(11分)
①(11分)令
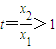 ,则①化为
,则①化为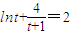 ②
②令
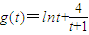 (t>1)
(t>1)∵
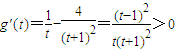
∴g(t)在(1,+∞)为增函数 (15分)
又t>1∴g(t)>g(1)=2此与②矛盾,
∴不存在 (16分)
点评:本题以函数为载体,考查导数的运用,考查函数的单调性,考查存在性问题,关键是对新定义的理解.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
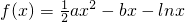 ,a>0,f'(1)=0.
,a>0,f'(1)=0.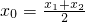 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图象上是否存在两点A、B,使得AB存在“中值伴随切线”?若存在,求出A、B的坐标;若不存在,说明理由.
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图象上是否存在两点A、B,使得AB存在“中值伴随切线”?若存在,求出A、B的坐标;若不存在,说明理由.