题目内容
已知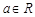 ,函数
,函数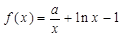 ,
,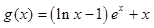 (其中
(其中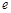 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数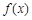 在
在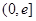 上的单调性;
上的单调性;
(2)是否存在实数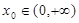 ,使曲线
,使曲线 在点
在点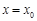 处的切线与
处的切线与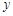 轴垂直? 若存在,
轴垂直? 若存在,
求出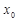 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若实数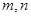 满足
满足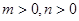 ,求证:
,求证: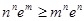 。
。
【答案】
(1)∵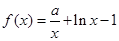 ,
,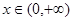 ,∴
,∴ . ……(1分)
. ……(1分)
①若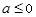 ,则
,则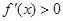 ,
,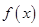 在
在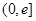 上单调递增;
……(2分)
上单调递增;
……(2分)
②若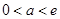 ,当
,当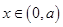 时,
时,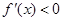 ,函数
,函数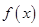 在区间
在区间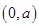 上单调递减,
上单调递减,
当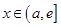 时,
时,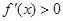 ,函数
,函数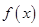 在区间
在区间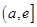 上单调递增,
……(4分)
上单调递增,
……(4分)
③若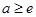 ,则
,则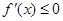 ,函数
,函数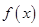 在区间
在区间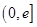 上单调递减. ……(5分)
上单调递减. ……(5分)
(2)解:∵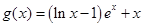 ,
,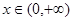 ,
,
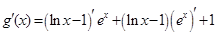
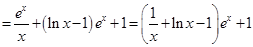 , ……(6分)
, ……(6分)
由(1)易知,当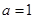 时,
时,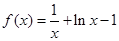 在
在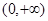 上的最小值:
上的最小值: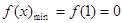 ,
,
即 时,
时,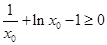 .
…(7分)
.
…(7分)
又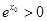 ,∴
,∴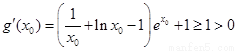 .…8分
.…8分
曲线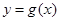 在点
在点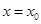 处的切线与
处的切线与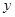 轴垂直等价于方程
轴垂直等价于方程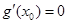 有实数解.
有实数解.
而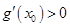 ,即方程
,即方程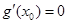 无实数解.故不存在.
……(9分)
无实数解.故不存在.
……(9分)
(3)证明: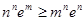
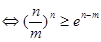
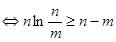
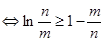
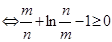 ,由(2)知
,由(2)知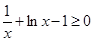 ,令
,令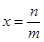 得
得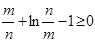 .……(14分)
.……(14分)
【解析】略

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
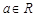 ,函数
,函数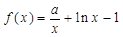 ,
,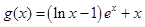 (其中
(其中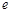 为自然对数的底数).
为自然对数的底数).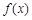 在
在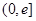 上的单调性;
上的单调性;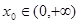 ,使曲线
,使曲线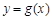 在点
在点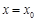 处的切线与
处的切线与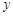 轴垂直? 若存在,
轴垂直? 若存在,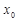 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;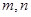 满足
满足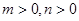 ,求证:
,求证: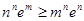 .
. ,函数
,函数 ,(其中
,(其中 为自然对数的底数).
为自然对数的底数). 在
在 上的单调性;
上的单调性; ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与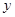 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数 在区间
在区间 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.