题目内容
已知![]() ,函数
,函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(2)是否存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直? 若存在,求出
轴垂直? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无最小值;
上无最小值;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
(2) 不存在![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直
轴垂直
解析:
(1)解:∵![]() ,∴
,∴![]() .
.
令![]() ,得
,得![]() .
.
①若![]() ,则
,则![]() ,
,![]() 在区间
在区间![]() 上单调递增,此时函数
上单调递增,此时函数![]() 无最小值.
无最小值.
②若![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
③若![]() ,则
,则![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
综上可知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无最小值;
上无最小值;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
(2)解:∵![]() ,
,![]() ,
,
∴ ![]()
![]() .
.
由(1)可知,当![]() 时,
时,![]() .
.
此时![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,即
,即![]() .
.
当![]() ,
,![]() ,
,![]() ,
,
∴ .
.
曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直等价于方程
轴垂直等价于方程![]() 有实数解.
有实数解.
而![]() ,即方程
,即方程![]() 无实数解.
无实数解.
故不存在![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.
轴垂直.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
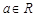 ,函数
,函数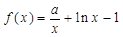 ,
,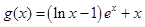 (其中
(其中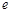 为自然对数的底数).
为自然对数的底数).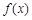 在
在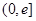 上的单调性;
上的单调性;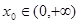 ,使曲线
,使曲线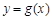 在点
在点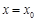 处的切线与
处的切线与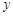 轴垂直? 若存在,
轴垂直? 若存在,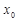 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;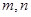 满足
满足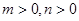 ,求证:
,求证: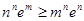 .
. ,函数
,函数 ,(其中
,(其中 为自然对数的底数).
为自然对数的底数). 在
在 上的单调性;
上的单调性; ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与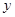 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. ,函数
,函数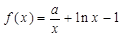 ,
,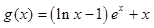 (其中
(其中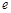 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数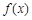 在
在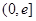 上的单调性;
上的单调性;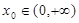 ,使曲线
,使曲线 在点
在点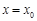 处的切线与
处的切线与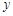 轴垂直? 若存在,
轴垂直? 若存在,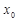 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.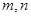 满足
满足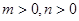 ,求证:
,求证: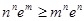 。
。 ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数 在区间
在区间 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.