题目内容
(本小题满分12分)
如图,棱长为2的正方体 中,E,F满足
中,E,F满足 .
.
(Ⅰ)求证:EF//平面AB ;
;
(Ⅱ)求证:EF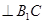 ;
;
(1)要证明线面平行,一般通过线线平行来证明,E、F分别为DD1、BD的中点,则可知中位线性质则EF∥BD1,进而根据线面平行的判定定理来证明。
(2)根据题意,由于AB⊥面BB1C1C 则可知AB⊥B1C且有B1C⊥BC1,AB∥BC1,那么得到B1C⊥面ABC1D,然后
结合线面垂直的性质定理来证明线线垂直。
解析试题分析:解: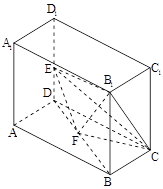
⑴∵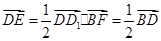
∴E、F分别为DD1、BD的中点…………2分
连结BD1,则EF∥BD1………………4分
又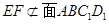 ……………………5分
……………………5分
∴EF∥面ABC1D1……………………6分
⑵正方体ABCD-A1B1C1D1中
∵AB⊥面BB1C1C ∴AB⊥B1C…………8分
又正方形BB1C1C中,B1C⊥BC1,AB∥BC1=B……10分
∴B1C⊥面ABC1D1
∴B1C⊥BD1
∵EF∥BD1
∴EF⊥B1C……………………12分
考点:本试题考查了线面的平行和垂直的证明题。
点评:解决空间中线线的平行和垂直的关键是对于线面的平行性质定理和线面的垂直的性质定理的熟练的运用,同时要结合平行的传递性来研究其它 的垂直问题。这类问题的解决一般要转化到一个平面中来分析,转化思想是立体几何的思想体现。中档题。

练习册系列答案
相关题目
 的底面
的底面 为平行四边形,
为平行四边形, 分别是棱
分别是棱 的中点,平面
的中点,平面 与平面
与平面 交于
交于 ,求证:
,求证:
 平面
平面 、
、 分别是
分别是 、
、 的中点,
的中点, 是
是 上的一动点,主视图与俯视图都为正方形。
上的一动点,主视图与俯视图都为正方形。

 ;
; 时,在棱
时,在棱 上确定一点
上确定一点 ,使得
,使得 ∥平面
∥平面 ,并给出证明。
,并给出证明。 的平面角余弦值。
的平面角余弦值。 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点,  ,且
,且 .将梯形
.将梯形 折成直二面角
折成直二面角 ,如图2所示.
,如图2所示.
 平面
平面 ;
; 关于点
关于点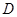 的对称点为
的对称点为 ,点
,点 在
在 所在平面内,且直线
所在平面内,且直线 与平面
与平面 所成的角为
所成的角为 ,试求出点
,试求出点 的最短距离.
的最短距离. 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
.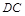 ⊥平面
⊥平面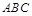 ,
,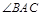 =90°,
=90°,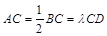 ,点
,点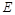 在
在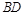 上,点E在BC上的射影为F,且
上,点E在BC上的射影为F,且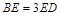 .
.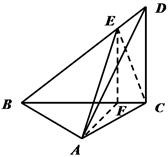
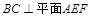 ;
;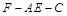 的大小为45°,求
的大小为45°,求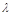 的值.
的值.
 中,
中, 为
为 边上的高,
边上的高, ,
, ,沿
,沿 翻折,使得
翻折,使得 ,得到几何体
,得到几何体 。
。
 ;
; 与平面
与平面 所成角的正切值。
所成角的正切值。
 的长; (2)求cos<
的长; (2)求cos< >的值; (3)求证:A1B⊥C1M.
>的值; (3)求证:A1B⊥C1M.