题目内容
.已知函数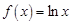 ,若存在
,若存在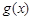 使得
使得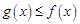 恒成立,则称
恒成立,则称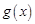 是
是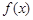 的一个“下界函数”
.
的一个“下界函数”
.
(I)如果函数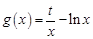 (
(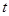 为实数)为
为实数)为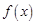 的一个“下界函数”,求
的一个“下界函数”,求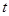 的取值范围;
的取值范围;
(II)设函数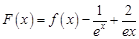 ,试问函数
,试问函数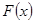 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
【答案】
(Ⅰ)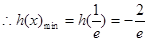
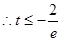 ;(Ⅱ)函数
;(Ⅱ)函数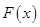 不存在零点.
不存在零点.
【解析】(I)本小题实质是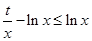 恒成立,即
恒成立,即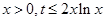 恒成立,然后利用导数
恒成立,然后利用导数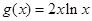 的最小值即可.
的最小值即可.
(II)在(I)的基础上,可知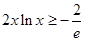
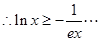
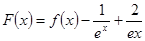 ,
,
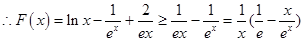 ,然后再构造函数
,然后再构造函数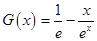 ,利用导数研究其最小值为
,利用导数研究其最小值为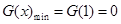 ,从而可知
,从而可知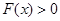 ,从而证明F(x)无零点.
,从而证明F(x)无零点.
(Ⅰ)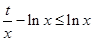 恒成立,
恒成立,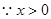 ,
, , ……………2分
, ……………2分
令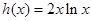 ,则
,则 ,
……………4分
,
……………4分
当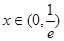 时,
时,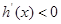 ,
,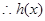 在
在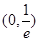 上是减函数,当
上是减函数,当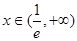 时,
时,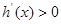 ,
,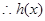 在
在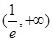 上是增函数,
……………6分
上是增函数,
……………6分
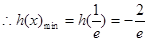
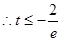 ……………7分
……………7分
(Ⅱ)由(I)知,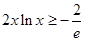
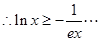
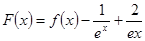 ①,
①,
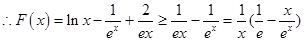 ,
……………10分
,
……………10分
令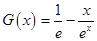 ,则
,则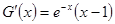 ,
……………12分
,
……………12分
则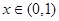 时,
时,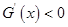 ,
,
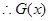 上是减函数,
上是减函数,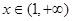 时,
时,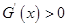 ,
,
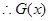 上是增函数,
上是增函数,
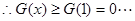 ②,
……………14分
②,
……………14分
 ,
,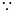 ①②中等号取到的条件不同,
①②中等号取到的条件不同,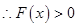 ,
,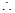 函数
函数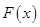 不存在零点.
……………15分
不存在零点.
……………15分

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 .
. ,求使
,求使 时
时 的取值范围;
的取值范围; 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围. ,若存在实数
,若存在实数 使
使 成立,则m的取值范围为( )
成立,则m的取值范围为( ) B、
B、
 C、
C、 D、
D、
 ,若存在正常数
,若存在正常数 ,使
,使 ,则不等式
,则不等式 的解集是_________。
的解集是_________。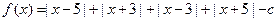 ,若存在正常数
,若存在正常数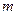 ,使
,使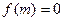 ,则不等式
,则不等式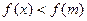 的解集是_________。
的解集是_________。